题目内容
19.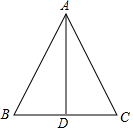 如图,在△ABC中,AB=AC,AD平分∠BAC.
如图,在△ABC中,AB=AC,AD平分∠BAC.(1)求证:△ABD≌△ACD.
(2)求证:AD⊥BC.
分析 (1)由条件利用SAS可证明△ABD≌△ACD;
(2)由(1)可得出∠ADB=∠ADC,结合平角的定义可求得∠ADB=90°,可证得结论.
解答 证明:
(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$
∴△ABD≌△ACD;
(2)∵△ABD≌△ACD,
∴∠ADB=∠ADC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
相关题目
10.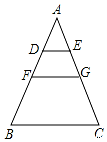 如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
 如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )| A. | 1:8:27 | B. | 1:4:9 | C. | 1:8:36 | D. | 1:9:36 |
11. a,b,c在数轴上的位置如图所示,则下列说法正确的是( )
a,b,c在数轴上的位置如图所示,则下列说法正确的是( )
 a,b,c在数轴上的位置如图所示,则下列说法正确的是( )
a,b,c在数轴上的位置如图所示,则下列说法正确的是( )| A. | a,b,c是负数 | B. | a,b,c是正数 | ||
| C. | a,b是负数,c是正数 | D. | a是负数,b,c是正数 |
8.实数$\frac{22}{7}$,$\sqrt{8}$,1.412,$\frac{2}{3}$π,$\sqrt{16}$,1.2020020002…,$\root{3}{27}$,0.121121112,2-$\sqrt{5}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.某食品厂从生产的袋装食品中抽出样品8袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正数、负数来表示,记录如表:
(1)这批样品的总质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
| 与标准质量的差值(单位:克) | -3 | -1 | 0 | 2 |
| 袋数 | 1 | 2 | 3 | 2 |
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?