Question

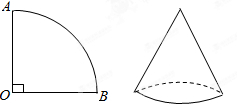如图，已知扇形OAB的圆心角为90°，半径为4厘米，求用这个扇形卷成的圆锥的高及圆锥的全面积．

Answer 1

分析：先利用弧长公式和扇形的面积公式计算弧AB=

90π•4

180

=2π，扇形OAB的面积=

90•π•42

360

=4π，利用扇形的弧长等于圆锥的底面圆的周长得到2π•DC=2π，则DC=1，可计算出圆锥的底面圆的面积为π，由扇形的半径等于圆锥的母线长得到SC=4，然后利用勾股定理可计算出高SD．

解答：解：如图，点D为圆锥底面圆的圆心，
∵扇形OAB的圆心角为90°，半径为4厘米，
∴弧AB=

90π•4

180

=2π，扇形OAB的面积=

90•π•42

360

=4π，
∴2π•DC=2π，
∴DC=1，
∴圆D的面积=π•1²=π，
在RtSDC中，SC=4，
SD=

SC2-DC2

=

42-12

=

15

，
∴用这个扇形卷成的圆锥的高为

15

cm，圆锥的全面积为（π+4π）=5πcm²．

点评：本题考查了圆锥的计算：圆锥的侧面展开图为扇形，扇形的弧长等于圆锥的底面圆的周长，扇形的半径等于圆锥的母线长．也考查了弧长公式和扇形的面积公式．