题目内容
17. 如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,将△AOB沿直线AB翻折,点O落在点O′处,则点O′的坐标为($\frac{4}{5}$,$\frac{8}{5}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,将△AOB沿直线AB翻折,点O落在点O′处,则点O′的坐标为($\frac{4}{5}$,$\frac{8}{5}$).
分析 根据已知条件得到OA=2,OB=1,根据折叠的性质得到AO′=AO=2,BO′=BO=1,∠AO′B=90°,延长AC交y轴于C,过O′作O′D⊥OA于D,根据相似三角形的性质得到BC=$\frac{5}{3}$,CO′=$\frac{4}{3}$,得到OC=$\frac{8}{3}$,AC=$\frac{10}{3}$,根据O′D∥OC,得到△ADO′∽△AOC,根据相似三角形的性质即可得到结论.
解答  解:在y=-$\frac{1}{2}$x+1中,令x=0,得y=1,令y=0,得x=2,
解:在y=-$\frac{1}{2}$x+1中,令x=0,得y=1,令y=0,得x=2,
∴A(2,0),B(0,1),
∴OA=2,OB=1,
∵将△AOB沿直线AB翻折,点O落在点O′处,
∴AO′=AO=2,BO′=BO=1,∠AO′B=90°,
延长AC交y轴于C,
过O′作O′D⊥OA于D,
∴∠CO′B=∠AOC=90°,
∵∠BCO′=∠ACO,
∴△BCO′∽△ACO,
∴$\frac{CO′}{OC}=\frac{O′B}{OA}=\frac{BC}{AC}$,
∴$\frac{CO′}{1+BC}$=$\frac{1}{2}$=$\frac{BC}{2+OC}$,
∴BC=$\frac{5}{3}$,CO′=$\frac{4}{3}$,
∴OC=$\frac{8}{3}$,AC=$\frac{10}{3}$,
∵O′D⊥OA,
∴O′D∥OC,
∴△ADO′∽△AOC,
∴$\frac{DO′}{OC}$=$\frac{AO′}{AC}$=$\frac{AD}{AO}$,即$\frac{DO′}{\frac{8}{3}}$=$\frac{2}{\frac{10}{3}}$=$\frac{AD}{2}$,
∴DO′=$\frac{8}{5}$,AD=$\frac{6}{5}$,
∴OD=$\frac{4}{5}$,
∴O′($\frac{4}{5}$,$\frac{8}{5}$),
故答案为:($\frac{4}{5}$,$\frac{8}{5}$).
点评 本题考查了一次函数图象上点的坐标特征,折叠的性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 1.450×10 | B. | 1.450×105 | C. | 14.50×104 | D. | 0.1450×106 |
| A. | 5 | B. | -3 | C. | 0 | D. | -6 |
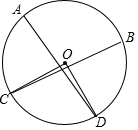 如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )
如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )| A. | 90° | B. | 45° | C. | 80° | D. | 70° |
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
| A. | 12.5×108 | B. | 12.5×109 | C. | 1.25×108 | D. | 1.25×109 |
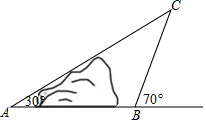 如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)
如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)