题目内容
按下列条件求代数式(a+b)(a2-ab+b2)与a3+b3的值,并根据计算的结果写出你发现的结论.
(1)a=3,b=1; (2)a=2 ,b=1
,b=1 .
.
解:(1)当a=3,b=1时,
(a+b)(a2-ab+b2)
=(3+1)(32-3×1+12)
=4×7
=28,
a3+b3=33+13
=27+1
=28;
即(a+b)(a2-ab+b2)=a3+b3.
(2)当a=2 =
= ,b=1
,b=1 =
= 时,
时,
(a+b)(a2-ab+b2)
=( +
+ )[
)[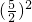 -
- ×
× +
+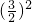 ]
]
=4× =19,
=19,
a3+b3= +
+ =
=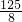 +
+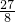 =19,
=19,
结论是(a+b)(a2-ab+b2)=a3+b3.
分析:(1)把a=3,b=1分别代入(a+b)(a2-ab+b2)与a3+b3求出即可;
(2)把a=2 ,b=1
,b=1 分别代入(a+b)(a2-ab+b2)与a3+b3求出即可;根据求出的结果即可得出结论.
分别代入(a+b)(a2-ab+b2)与a3+b3求出即可;根据求出的结果即可得出结论.
点评:本题考查了求代数式的值,关键是能根据求出的结果得出结论.
(a+b)(a2-ab+b2)
=(3+1)(32-3×1+12)
=4×7
=28,
a3+b3=33+13
=27+1
=28;
即(a+b)(a2-ab+b2)=a3+b3.
(2)当a=2
 =
= ,b=1
,b=1 =
= 时,
时,(a+b)(a2-ab+b2)
=(
 +
+ )[
)[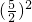 -
- ×
× +
+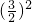 ]
]=4×
 =19,
=19,a3+b3=
 +
+ =
=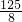 +
+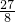 =19,
=19,结论是(a+b)(a2-ab+b2)=a3+b3.
分析:(1)把a=3,b=1分别代入(a+b)(a2-ab+b2)与a3+b3求出即可;
(2)把a=2
 ,b=1
,b=1 分别代入(a+b)(a2-ab+b2)与a3+b3求出即可;根据求出的结果即可得出结论.
分别代入(a+b)(a2-ab+b2)与a3+b3求出即可;根据求出的结果即可得出结论.点评:本题考查了求代数式的值,关键是能根据求出的结果得出结论.

练习册系列答案
相关题目
 -ab+
-ab+ )与
)与 的值,并根据计算结果写出你发现的结论.
的值,并根据计算结果写出你发现的结论. ,b=
,b= .
.