题目内容
18. 反比例函数y=$\frac{k}{x}$的图象与直线y=-x-(k+1))相交与A、C两点,点A在第二象限,过A作AB⊥x轴于点B,且S△ABO=1.5.
反比例函数y=$\frac{k}{x}$的图象与直线y=-x-(k+1))相交与A、C两点,点A在第二象限,过A作AB⊥x轴于点B,且S△ABO=1.5.(1)求A、C两点的坐标;
(2)求△AOC的面积;
(3)根据图象写出使一次函数值大于反比例函数值的x的取值范围.
分析 (1)根据反比例函数的性质,利用S△ABO=1.5,即可得出xy=-3,进而求出一次函数解析式,将两函数解析式联立求出交点坐标即可,根据A,C两点坐标;
(2)根据A,C的坐标即可得出△AOC的面积;
(3)利用函数图象的交点坐标即可得出一次函数的值小于反比例函数的值时自变量x的取值范围.
解答 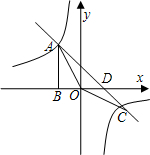 解:(1)设A点坐标为(x,y)且x<0,y>0,
解:(1)设A点坐标为(x,y)且x<0,y>0,
则S△AB0=$\frac{1}{2}$|BO||BA|=$\frac{1}{2}$(-x)y=$\frac{3}{2}$,
∴xy=-3,
又∵y=$\frac{k}{x}$,xy=k,
∴k=-3,
∴所求的两个函数的解析式分别为y=-$\frac{3}{x}$,y=-x+2;
(2)由y=-x+2,令y=0得x=2.
直线y=-x+2与x轴的交点D的坐标为(2,0).
由$\left\{\begin{array}{l}{y=-x+2}\\{y=-\frac{3}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,
∴A(-1,3),C(3,-1),
(2)∵A(-1,3),C(3,-1),
∴S△AOC=S△AOD+S△ODC=4,
(3)∵A(-1,3),C(3,-1),
∴当x>3或-1<x<0时
∴当-1<x<0或x>3时,一次函数的值小于反比例函数的值.
点评 本题考查的是反比例函数与一次函数的交点问题,熟知反比例函数中k=xy是定值这一知识点是解答此题的关键.

练习册系列答案
相关题目
20.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是13,则每个支干长出( )
| A. | 2根小分支 | B. | 3根小分支 | C. | 4根小分支 | D. | 5根小分支 |
1.下列各组单项式中,是同类项的是( )
| A. | 2x3与3x2 | B. | a3与b3 | C. | 2x2y与2xy2 | D. | 23与32 |
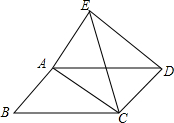 如图,平行四边形ABCD中,∠ACB=30°,将△ABC沿AC折叠,使得点B落在平行四边形ABCD所在的平面的点E处,则$\frac{AC+DE}{AD}$=$\sqrt{3}$.
如图,平行四边形ABCD中,∠ACB=30°,将△ABC沿AC折叠,使得点B落在平行四边形ABCD所在的平面的点E处,则$\frac{AC+DE}{AD}$=$\sqrt{3}$. 如图,C是线段AB的中点,D是线段BC的中点.
如图,C是线段AB的中点,D是线段BC的中点.