题目内容
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从 左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题:
左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题:(1)这次共抽调了多少人?
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少?
(3)如果这次测试成绩的中位数是120次,那么这次测试中,成绩为120次的学生至少有多少人?
分析:(1)根据题意:结合各小组频数之和等于数据总和,各小组频率之和等于1;易得第二组的频率0.08;再由频率、频数的关系频率=
;可得总人数.
(2)根据题意:从左至右第二、三、四组的频数比为4:17:15,和(1)的结论;容易求得各组的人数,这样就能求出优秀率.
(3)由中位数的意义,作答即可.
| 频数 |
| 数据总和 |
(2)根据题意:从左至右第二、三、四组的频数比为4:17:15,和(1)的结论;容易求得各组的人数,这样就能求出优秀率.
(3)由中位数的意义,作答即可.
解答:解:(1)第一组的频率为1-0.96=0.04,
第二组的频率为0.12-0.04=0.08,
故总人数为
=150(人),即这次共抽调了150人;
(2)第一组人数为150×0.04=6(人),第三、四组人数分别为51人、45人,
这次测试的优秀率为
×100%=24%;
(3)前三组的人数为69,而中位数是第75和第76个数的平均数,而120是第四组中最小的数值,因而第75和第76都是120,所以成绩为120次的学生至少有76-69=7人.
第二组的频率为0.12-0.04=0.08,
故总人数为
| 12 |
| 0.08 |
(2)第一组人数为150×0.04=6(人),第三、四组人数分别为51人、45人,
这次测试的优秀率为
| 150-6-12-51-45 |
| 150 |
(3)前三组的人数为69,而中位数是第75和第76个数的平均数,而120是第四组中最小的数值,因而第75和第76都是120,所以成绩为120次的学生至少有76-69=7人.
点评:本题考查了中位数的运用和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.同时对频率、频数灵活运用的综合考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系频率=
.
| 频数 |
| 数据总和 |

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
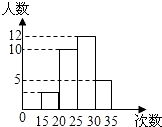 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起座次数在15~20次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起座次数在15~20次之间的频率是( )| A、0.1 | B、0.17 | C、0.33 | D、0.4 |
 15、某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐次数在20~25次之间的频数是
15、某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐次数在20~25次之间的频数是 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,统计图如图所示,则本次测试共抽调人数为( )
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,统计图如图所示,则本次测试共抽调人数为( ) (2007•海淀区二模)某校为了了解九年级学生的体能素质,在400名学生中随机选择部分学生进行测试,其中一项为立定跳远.有关数据整理如下:
(2007•海淀区二模)某校为了了解九年级学生的体能素质,在400名学生中随机选择部分学生进行测试,其中一项为立定跳远.有关数据整理如下: