题目内容
 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出第二组的频率是0.08,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出第二组的频率是0.08,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:(1)这次共抽调了多少人?
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少?
(3)若该校九年级有600名学生,请估计该校九年级达到优秀的人数是多少?
分析:(1)利用频数=总数×频率可得抽调的总人数;
(2)首先计算出前四个小组的人数,再用总数减去前四个小组的人数可得后两个小组的人数和,再计算出优秀率即可;
(3)利用样本估计总体的方法即可算出答案.
(2)首先计算出前四个小组的人数,再用总数减去前四个小组的人数可得后两个小组的人数和,再计算出优秀率即可;
(3)利用样本估计总体的方法即可算出答案.
解答:解:(1)共抽调的人数:12÷0.08=150(人);
(2)∵第一、二、三、四组的频数比为2:4:17:15,第二小组的频数为12,
∴第一、三、四组的频数分别为:6,51,45,
∴第五、六小组的频数和为:150-(6+12+51+45)=36,
这次测试成绩的优秀率是:
×100%=24%;
(3)600×24%=144(人).
答:该校九年级达到优秀的人数是144人.
(2)∵第一、二、三、四组的频数比为2:4:17:15,第二小组的频数为12,
∴第一、三、四组的频数分别为:6,51,45,
∴第五、六小组的频数和为:150-(6+12+51+45)=36,
这次测试成绩的优秀率是:
| 36 |
| 150 |
(3)600×24%=144(人).
答:该校九年级达到优秀的人数是144人.
点评:此题主要考查了读频数分布直方图的能力和利用统计图获取信息的能力,以及样本估计总体,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.各小组频数之和等于数据总和,各小组频率之和等于1.

练习册系列答案
相关题目
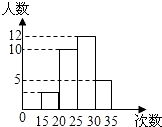 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起座次数在15~20次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起座次数在15~20次之间的频率是( )| A、0.1 | B、0.17 | C、0.33 | D、0.4 |
 15、某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐次数在20~25次之间的频数是
15、某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐次数在20~25次之间的频数是 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,统计图如图所示,则本次测试共抽调人数为( )
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,统计图如图所示,则本次测试共抽调人数为( ) (2007•海淀区二模)某校为了了解九年级学生的体能素质,在400名学生中随机选择部分学生进行测试,其中一项为立定跳远.有关数据整理如下:
(2007•海淀区二模)某校为了了解九年级学生的体能素质,在400名学生中随机选择部分学生进行测试,其中一项为立定跳远.有关数据整理如下: