题目内容
如图,等腰梯形ABCD中,AD∥BC,∠B=45°,P是BC边上一点,△PAD的面积为 ,设AB=x,AD=y
,设AB=x,AD=y
(1)求y与x的函数关系式;
(2)若∠APD=45°,当y=1时,求PB•PC的值;
(3)若∠APD=90°,求y的最小值.

(1)如图1,过A作AE⊥BC于点E,在Rt△ABE中,∠B=45°,AB=x,
∴AE=AB•sinB= x,∵S△APD=
x,∵S△APD= AD•AE=
AD•AE= ,
,
∴ •y•
•y• x=
x= , 则y=
, 则y= ;
;
(2)∵∠APC=∠APD+∠CPD=∠B+∠BAP,∠APD=∠B=45°,
∴∠BAP=∠CPD,∵四边形ABCD为等腰梯形,∴∠B=∠C,AB=CD,
∴△ABP∽△PCD,∴ =
= ,∴PB•PC=AB•DC=AB2,
,∴PB•PC=AB•DC=AB2,
当y=1时,x= ,即AB=
,即AB= ,则PB•PC=(
,则PB•PC=( )2=2;
)2=2;
(3)如图2,取AD的中点F,连接PF,过P作PH⊥AD,可得PF≥PH,
当PF=PH时,PF有最小值,∵∠APD=90°,∴PF=AD=y,∴PH=y,
∵S△APD= •AD•PH=
•AD•PH= ,∴
,∴ •y•
•y• y=
y= ,即y2=2,∵y>0,∴y=
,即y2=2,∵y>0,∴y= ,
,
则y的最小值为 .
.

练习册系列答案
相关题目
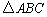 中,
中, ,
, 平分
平分 ,CD=1 cm,那么
,CD=1 cm,那么 点到边
点到边 所在直线的距离是 cm.
所在直线的距离是 cm.

 B.
B. C.
C. D.
D.
 B.
B. C.
C.  D.
D.