题目内容
如图在Rt△ABC中，∠ACB=90°，BC=3，AB=5，则下列结论正确的是
- A.sinA=
- B.tanA=
- C.cosB=
- D.tanB=
D
分析：首先利用勾股定理计算出AC的长，再根据三角函数定义进行计算即可选出答案．
解答：∵在Rt△ABC中，∠ACB=90°，BC=3，AB=5，
∴AC=
=4，
∴sinA=
=，tanA=
=
，cosB=，tanB=，
故选：D．
点评：本题主要考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
分析：首先利用勾股定理计算出AC的长，再根据三角函数定义进行计算即可选出答案．
解答：∵在Rt△ABC中，∠ACB=90°，BC=3，AB=5，
∴AC=
=4，∴sinA=
=，tanA==，cosB=，tanB=，故选：D．
点评：本题主要考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
相关题目
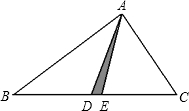如图在Rt△ABC中，∠BAC=90°，AB=5，AC=4，AD、AE分别是△ABC的中线和角平分线，则△ADE的面积为
如图在Rt△ABC中，∠ACB=90°，sinA=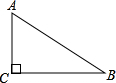
如图在Rt△ABC中，∠C=90°，AC=5，AB=13，则tanB=
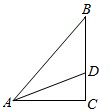如图在Rt△ABC中，AD平分∠CAB，CD=8cm，那么点D到AB的距离是
（1）如图在Rt△ABC中，CD是AB边上的高，若AD=8，BD=2，则CD=