题目内容
【题目】对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的"距离",记作d(M,N) . 特别的,当图形M,N有公共点时,记作d(M,N)=0.一次函数y=kx+2的图像为L,L 与y 轴交点为D, △ABC中,A(0,1),B(-1,0),C(1,0).
(1)求d(点 D , △ABC)= ;当k=1时,求d( L , △ABC)= ;
(2)若d(L, △ABC)=0.直接写出k的取值范围;
(3)函数y=x+b的图像记为W , 若d(W,△ABC) ![]() 1 ,求出b的取值范围.
1 ,求出b的取值范围.
【答案】(1)d(点 D , △ABC)=1 , d( L , △ABC)= ![]() ;(2)k≥2或k≤-2 .;(3)d(W,△ABC)
;(2)k≥2或k≤-2 .;(3)d(W,△ABC) ![]() 1时,-1-
1时,-1-![]()
![]() b
b ![]() 1+
1+![]() .
.
【解析】
(1)根据新定义,转化为实际是求点D到点A的距离,当k=1时,求d(L,△ABC)实际是求两条平行线之间的距离,通过作垂线,转化为直角三角形用勾股定理求得;
(2)若d(L,△ABC)=0就是求直线L与三角形ABC有公共点,可以先考虑仅有一个公共点时k的值,然后根据一次函数的性质,求得k的取值范围;
(3)函数y=x+b的图象记为W,若d(W,△ABC)≤1就是求W到三角形ABC的距离小于或等于1,可以先求距离为1时的b的值,然后根据一次函数的性质,求得b的取值范围.
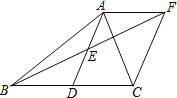
解:(1)一次函数y=kx+2的图象与y轴交点D(0,2),
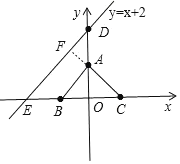
d(点D,△ABC)表示点D到△ABC的最小距离,就是点D到点A的距离,即:AD=21=1,
∴d(点D,△ABC)=1
当k=1时,直线y=x+2,此时直线L与AB所在的直线平行,且△ABC和△DOE均是等腰直角三角形,
d(L,△ABC)表示直线L到△ABC的最小距离,就是图中的AF,
在等腰直角三角形ADF中,AD=1,AF=1×![]() ,d(L,△ABC)=
,d(L,△ABC)=![]() ,
,
故答案为:1,![]() ;
;
(2)若d(L,△ABC)=0.说明直线L:y=kx+2与△ABC有公共点,因此有两种情况,即:k>0或k<0,仅有一个公共点时如图所示,
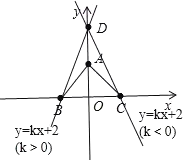
即直线L过B点,或过C点,
此时可求出k=2或k=2,根据直线L与△ABC有公共点,
∴k≥2或k≤2,
答:若d(L,△ABC)=0时.k的取值范围为:k≥2或k≤2.
(3)函数y=x+b的图象W与x轴、y轴交点所围成的三角形是等腰直角三角形,并且函数y=x+b的图象与AB平行,
当d(W,△ABC)=1
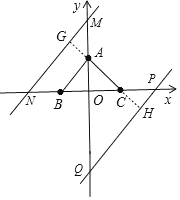
在△AGM中,AG=GM=1,则AM=![]() ,OM=1+
,OM=1+![]() ,M(0,1+
,M(0,1+![]() );即:b=1+
);即:b=1+![]() ;
;
同理:OQ=OP=1+![]() ,Q(0,1
,Q(0,1![]() ),即:b=1
),即:b=1![]() ,
,
若d(W,△ABC)≤1,即b的值在M、N之间,
∴1![]() ≤b≤1+
≤b≤1+![]() ,
,
答:若d(W,△ABC)≤1,b的取值范围为:1![]() ≤b≤1+
≤b≤1+![]() .
.

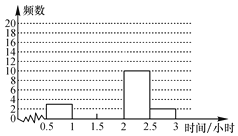
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
某区音乐成绩频数分布直方图
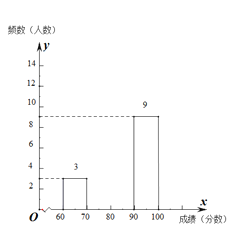
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.