题目内容
【题目】某厂按用户的月需求量
(件)完成一种产品的生产，其中
．每件的售价为18万元，每件的成本
(万元)是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量
(件)成反比．经市场调研发现，月需求量
与月份
(
为整数，
)符合关系式
(
为常数)，且得到了表中的数据．
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求
与
满足的关系式，请说明一件产品的利润能否是12万元；
(2)求
，并推断是否存在某个月既无盈利也不亏损；
(3)在这一年12个月中，若第
个月和第
个月的利润相差最大，求
．
【答案】(1)
，不可能；(2)不存在；(3)1或11.
【解析】
试题分析：(1)根据每件的成本y(万元)是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x(件)成反比，结合表格，用待定系数法求y与x之间的函数关系式，再列方程求解，检验所得结果是还符合题意；(2)将表格中的n，对应的x值，代入到
，求出k，根据某个月既无盈利也不亏损，得到一个关于n的一元二次方程，判断根的情况；(3)用含m的代数式表示出第m个月，第(m+1)个月的利润，再对它们的差的情况讨论.
试题解析：(1)由题意设
，由表中数据，得
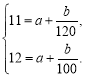解得
∴.
由题意，若
，则
.
∵x＞0，∴
.
∴不可能.
(2)将n=1，x=120代入
，得
120=2-2k+9k+27.解得k=13.
将n=2，x=100代入
也符合.
∴k=13.
由题意，得18=6+
，求得x=50.
∴50=
，即
.
∵
，∴方程无实数根.
∴不存在.
(3)第m个月的利润为w=
=
；
∴第(m+1)个月的利润为
W′=
.
若W≥W′，W-W′=48(6-m),m取最小1，W-W′=240最大.
若W＜W′，W′-W=48(m-6),m+1≤12，m取最大11，W′-W=240最大.
∴m=1或11.
