题目内容
【题目】如图，在四边形
中，
，顶点
是原点，顶点
在
轴上，顶点
的坐标为
，
,
，点
从点出发，以
的速度向点
运动，点
从点同时出发，以
的速度向点运动.规定其中一个动点到达端点时，另一个动点也随之停止运动；从运动开始，设
点运动的时间为
.
求直线
的函数解析式；
当
为何值时，四边形
是矩形？
【答案】（1）
；（2）
为
.
【解析】
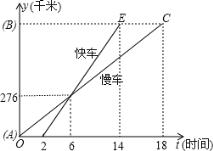
(1)首先根据顶点A的坐标为（0，8），AC=24cm，OB=26cm，分别求出点B、C的坐标各是多少；然后应用待定系数法，求出直线BC的函数解析式即可．
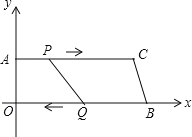
(2)根据四边形AOQP是矩形，可得AP=OQ，据此求出t的值是多少即可．
解：
如图1，
顶点
的坐标为
，
，
，
，
设直线
的函数解析式是
，
则
解得
直线的函数解析式是．
如图2，
根据题意得：
，则
，
四边形
是矩形，
，
，
解得
，
当为时，四边形是矩形.
练习册系列答案
相关题目
【题目】为了加强公民的节水意识，合理利用水资源，各地采取价格调控手段达到节约用水的目的，某市规定如下用水收费标准：每户每月的用水量不超过
立方米时，水费按每立方米
元收费，超过立方米时，不超过的部分每立方米仍按元收费，超过的部分每立方米按
元收费，该市某户今年
月份的用水量和所交水费如下表所示：
月份 | 用水量（ | 收费（元） |
|
|
|
|
|
|
设某户每月用水量
（立方米），应交水费
（元）
求
的值，当
时，分别写出与的函数关系式.
若该户
月份用水量为
立方米，求该月份水费多少元？
