Question

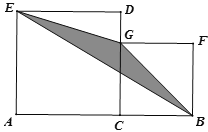
【题目】一幢房屋的侧面外墙壁的形状如图所示，它由等腰三角形OCD和矩形ABCD组成，∠OCD=25°，外墙壁上用涂料涂成颜色相同的条纹，其中一块的形状是四边形EFGH，测得FG∥EH，GH=2.6m，∠FGB=65°．

（1）求证：GF⊥OC；
（2）求EF的长（结果精确到0.1m）．
（参考数据：sin25°=cos65°≈0.42，cos25°=sin65°≈0.91）

Answer 1

【答案】
（1）证明：CD与FG交于点M，

∵∠OCD=25°，四边形ABCD是矩形，∠FGB=65°．

∴∠FMC=65°，

∴∠MFC=90°，

∴GF⊥CO

（2）解：作GN⊥EH于点N，

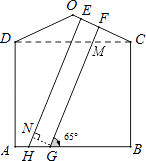
∵FG∥EH，GF⊥CO；

∴四边形ENGF是矩形；

∴EF=NG，

∵∠FGB=∠NHG=65°，

∴sin65°= = ≈0.91，

∴EF=NG=2.366m≈2.4m．

【解析】（1）根据∠OCD=25°，四边形ABCD是矩形，∠FGB=65°，得出∠FMC=65°，得∠MFC=90°，即证得GF⊥OC；
（2）根据矩形的判定得出EF=NG，再利用解直角三角形的知识得出NG的长，即可得到EF的长．