Question

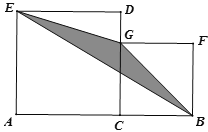
【题目】如图，点C是线段AB上的一点，分别以AC．BC为边在AB的同侧作正方形ACDE和正方形CBFG，连接EG．BG．BE，当BC＝1时，△BEG的面积记为S1，当BC＝2时，△BEG的面积记为S2，……，以此类推，当BC＝n时，△BEG的面积记为Sn，则S2020－S2019的值为____．

Answer 1

【答案】

【解析】

作辅助线，构建同底等高三角形，根据等腰直角三角形面积公式可得结论．

解：如图，连接EC，

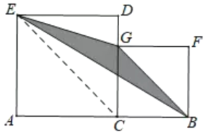
∵正方形ACDE和正方形CBFG，
∴∠ACE＝∠ABG＝45°，
∴EC∥BG，
∴△BCG和△BEG是同底（BG）等高的三角形，
即S△BCG＝S△BEG，
∴当BC＝n时，Sn＝n2，
∴S2020S2019＝×20202×20192＝（2020＋2019）（20202019）＝；
故答案为：．