题目内容
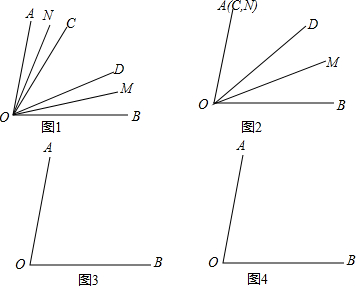 如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC
如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC(1)将图1中∠COD绕O点逆时针旋转,使射线OC与射线OA重合(∠AOC=0°,ON与OA重合,如图2),其他条件不变,请直接写出∠MON的度数
(2)将图2中的∠COD绕O点逆时针旋转α度,其他条件不变.
①当40°<α<100°,请完成图3,并求∠MON的度数;
②当140°<α<180°,请完成图4,并求∠MON的度数.
考点:角的计算,角平分线的定义
专题:
分析:(1)根据角平分线的定义即可求得∠BOM的值,即可解题;
(2)①画出图形,即可求得∠CON、∠BOM的值,即可解题;
②画出图形,即可求得∠CON、∠DOM的值,即可解题.
(2)①画出图形,即可求得∠CON、∠BOM的值,即可解题;
②画出图形,即可求得∠CON、∠DOM的值,即可解题.
解答:解:(1)∵∠AOB=80°,∠COD=40°,
∴∠BOD=80°-40°=40°,
∵OM平分∠BOD,
∴∠BOM=
∠BOD=20°,
∴∠MON=∠AOB-∠BOM=60°;
(2)①画出图形,∠AOC=α,

∵∠AOC=α,∠AOB=80°,OM平分∠BOD,ON平分∠AOC
∴∠BOM=
∠BOD=
(∠AOB+∠AOC-∠COD)=
(40°+α),
∠CON=
∠AOC=
α,
∴∠MON=∠AOB+∠AOC-∠CON-∠BOM=80°+α-
α-
(40°+α)
=60°;
②作出图形,∠AOC=α,

则∠CON=
α,
∵∠BOD=∠BOC+COD=(360°-80°-α)+40°=320°-α,
∴∠MOD=
∠BOD=
(320°-α),
∴∠MON=∠MOD+∠CON-∠COD=
(320°-α)+
α-40°=120°.
∴∠BOD=80°-40°=40°,
∵OM平分∠BOD,
∴∠BOM=
| 1 |
| 2 |
∴∠MON=∠AOB-∠BOM=60°;
(2)①画出图形,∠AOC=α,

∵∠AOC=α,∠AOB=80°,OM平分∠BOD,ON平分∠AOC
∴∠BOM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠AOB+∠AOC-∠CON-∠BOM=80°+α-
| 1 |
| 2 |
| 1 |
| 2 |
=60°;
②作出图形,∠AOC=α,

则∠CON=
| 1 |
| 2 |
∵∠BOD=∠BOC+COD=(360°-80°-α)+40°=320°-α,
∴∠MOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠MOD+∠CON-∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角度数的计算,考查了角平分线平分角的性质,本题中准确画出图形是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
设a是方程x2+x-2009=0的一个实数根,则a2+a-1的值为( )
| A、2006 | B、2007 |
| C、2008 | D、2009 |
 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF; ②△EPF是等腰直角三角形; ③S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF; ②△EPF是等腰直角三角形; ③S四边形AEPF= 如图,已知C、D是AB上两点,且AB=20cm,CD=6cm,M是AD的中点,N是BC的中点,则线段MN的长为
如图,已知C、D是AB上两点,且AB=20cm,CD=6cm,M是AD的中点,N是BC的中点,则线段MN的长为 已知:如图,点C为线段AB上的一点,△ACM和△CBN是等边三角形,直线AN、CM交于点E,直线BM、CN交于点F.
已知:如图,点C为线段AB上的一点,△ACM和△CBN是等边三角形,直线AN、CM交于点E,直线BM、CN交于点F.