题目内容
 如图,已知C、D是AB上两点,且AB=20cm,CD=6cm,M是AD的中点,N是BC的中点,则线段MN的长为
如图,已知C、D是AB上两点,且AB=20cm,CD=6cm,M是AD的中点,N是BC的中点,则线段MN的长为考点:两点间的距离
专题:
分析:设AC=x,则BD=14-x,再用x表示出各线段的长度,再根据MN=AN-AM即可得出结论.
解答:解:∵AB=20cm,CD=6cm,
∴设AC=x,则BD=14-x,
∵M是AD的中点,N是BC的中点,
∴AM=DM=
(AC+CD)=
(x+6),BC=CD+BD=20-x,CN=BN=10-
x,
∴AN=CN+AC=10+
x,
∴MN=AN-AM=10+
x-
x-3=7(cm).
故答案为:7cm.
∴设AC=x,则BD=14-x,
∵M是AD的中点,N是BC的中点,
∴AM=DM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AN=CN+AC=10+
| 1 |
| 2 |
∴MN=AN-AM=10+
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:7cm.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
下列判断正确的是( )
| A、近似数0.380是精确到0.01 |
| B、近似数5.6万是精确到十分位 |
| C、近似数300是精确到百位 |
| D、近似数1.60×103是精确到十位 |
已知a+b=2,求代数式a2-b2+4b的值为( )
| A、8 | B、4 | C、-4 | D、-8 |
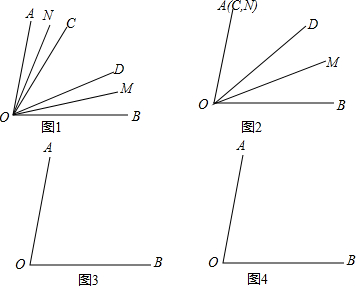 如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC
如图1,已知∠AOB=80°,∠COD=40°,OM平分∠BOD,ON平分∠AOC