题目内容
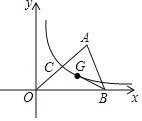
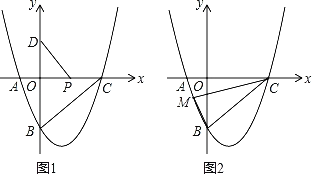
【题目】如图，一次函数y1＝kx+b的图象分别交x轴，y轴于A，B两点，交反比例函数y2＝
的图象于C，D两点，B（0，3），D（2，﹣1）．
（1）求一次函数与反比例函数的表达式；
（2）请直接写出当y2≥y1时，x的取值范围；
（3）点E为反比例函数y2＝的图象上一点，横坐标为m，若将点E向右平移2个单位后刚好落在一次函数y1＝kx+b的图象上，求m的值．
【答案】（1）一次函数的关系式为y＝﹣2x+3；反比例函数的关系式为y＝﹣
；（2）﹣
＜x＜0或x＞2；（3）
或
．
【解析】
（1）利用待定系数法求解一次函数与反比例函数的解析式即可；
（2）先把两个函数解析式联立求解
的坐标，再根据图像直接写出不等式的解集即可；
（3）利用含
的代数式分别表示
的坐标，利用平移的性质的两点的纵坐标不变，列方程求解即可．
解：（1）把B（0，3），D（2，﹣1）代入一次函数y1＝kx+b得，
，
解得：
∴一次函数的关系式为y＝﹣2x+3，
把D（2，﹣1）代入反比例函数关系式得，a＝2×（﹣1）＝﹣2，
∴反比例函数的关系式为y＝﹣；
（2）由题意得，
，
解得：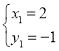
，
，
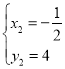∵D（2，﹣1），
∴C（﹣，4），
根据图象可知，当y2≥y1时，x的取值范围为﹣＜x＜0或x＞2．
（3）设平移后落在y＝﹣2x+3上的对应点为E′，
则E（m，﹣
），E′（m+2，﹣2m﹣1）
因此有：﹣＝﹣2m+1，
解得，m1＝，m2＝，
经检验，均符合题意，
故m的值为：或．
练习册系列答案
一线名师权威作业本系列答案
相关题目
