题目内容
16．
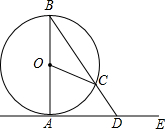如图，AB为⊙O的直径，点C在⊙O上，AD是⊙O的切线，A为切点，连接BC并延长交AD于点D，若∠AOC=80°，求∠ADB的度数．
分析 先根据切线的性质得∠BAD=90°，再利用三角形外角性质求出∠B，然后在Rt△ABD中利用互余计算∠ADB的度数．
解答 解：∵AD是⊙O的切线，
∴BA⊥AD，
∴∠BAD=90°，
∵OC=OB，
∴∠B=∠OCB，
而∠AOC=∠B+∠OCB，
∴∠B=$\frac{1}{2}∠$AOC=$\frac{1}{2}$×80°=40°，
在Rt△ABD中，∠ADB=90°-∠B=50°．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．
练习册系列答案
相关题目
已知：如图，AE⊥BC于M，FG⊥BC于N，∠1=∠2，∠D=∠3+50°，∠CBD=70°．