题目内容
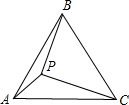 点P是等边△ABC内一点,且PA=2,
点P是等边△ABC内一点,且PA=2, ,PC=4,求∠APB的度数.(友情提示:将△APC绕A逆时针旋转60°得到△AP′B,连接PP′)
,PC=4,求∠APB的度数.(友情提示:将△APC绕A逆时针旋转60°得到△AP′B,连接PP′)
 解:将△APC绕点A逆时针旋转60°得到△AP′B,连接PP′,
解:将△APC绕点A逆时针旋转60°得到△AP′B,连接PP′,∵AP′=AP,∠P′AP=∠BAC=60°,
∴△AP′P为等边三角形,
∴PP′=PA=2,
又∵
 ,P′B=PC=4,
,P′B=PC=4,∴PB2+PP′2=BP′2,
∴∠BPP′=90°,
又∵∠P′PA=60°,
∴∠APB=∠BPP′+∠P′PA=90°+60°=150°.
分析:先依据题意作出简单的图形,不难得出△AP′P为等边三角形,再由线段之间的特殊关系,得出∠BPP′=90°,进而可求解∠APB.
点评:熟练掌握等边三角形的性质,能够利用其性质进行一些简单的计算.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.(提示:连接CE)
如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.(提示:连接CE)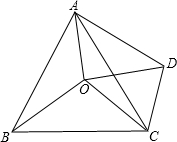 得△ADC,连接OD.
得△ADC,连接OD. 18、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
18、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.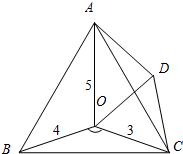 28、如图,点O是等边△ABC内一点,且OA=5,OB=4,OC=3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,回答下列问题:
28、如图,点O是等边△ABC内一点,且OA=5,OB=4,OC=3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,回答下列问题: 得到线段CD,连接OD、AD.
得到线段CD,连接OD、AD.