Question

如图，点E是等边△ABC内一点，且EA=EB，△ABC外一点D满足BD=AC，且BE平分∠DBC，求∠BDE的度数．（提示：连接CE）

Answer 1

分析：由已知条件先证明△BCE≌△ACE得到∠BCE=∠ACE=30°，再证明△BDE≌△BCE得到∠BDE=∠BCE=30°．

解答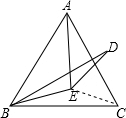：解：连接CE，
∵△ABC是等边三角形，
∴AC=BC，
在△BCE与△ACE中，

AC=BC AE=BE CE=CE

，
∴△BCE≌△ACE（SSS），
∴∠BCE=∠ACE=30°
∵BE平分∠DBC，
∴∠DBE=∠CBE，
在△BDE与△BCE中，

BD=BC ∠DBE=∠CBE BE=BE

，
∴△BDE≌△BCE，
∴∠BDE=∠BCE=30°．

点评：本题考查了全等三角形的判定与性质及等边三角形的性质；熟练掌握等边三角形的性质，会运用全等求解角相等，正确作出辅助线是解答本题的关键．