Question

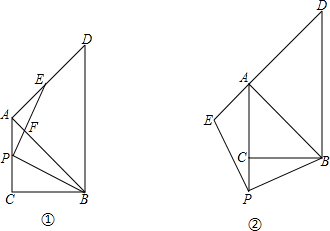
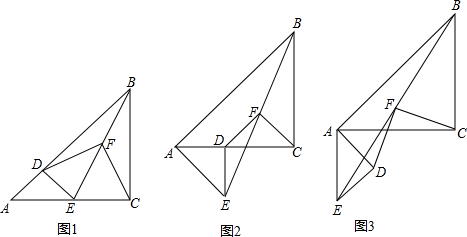
已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连结DF、CF.
【小题1】（1）如图1, 当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；
【小题2】（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；
【小题3】（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC=，求此时线段CF的长(直接写出结果).

Answer 1

【小题1】解：（1）线段DF、CF之间的数量和位置关系分别是相等和垂直.
【小题2】（2）（1）中的结论仍然成立.
证明：如图，此时点D落在AC上，延长DF交BC于点G.     ………2分………2分
∵ ，
∴ DE∥BC.
∴  .
又∵ F为BE中点，
∴ EF=BF.
∴ △DEF≌△GBF .             ………3分
∴ DE=GB,DF=GF.
又∵ AD=DE,AC=BC,
∴ DC=GC.
∵ ,
∴ DF = CF, DF⊥CF.  
【小题3】（3）线段C F的长为解析:
略