题目内容
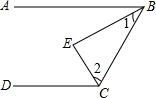 如图,BE平分∠ABC,CE平分∠BCD,BE垂直CE于点E,AB与DC平行吗?
如图,BE平分∠ABC,CE平分∠BCD,BE垂直CE于点E,AB与DC平行吗?∵BE平分∠ABC(已知)
∴
∵CE平分∠BCD(已知)
∴
∴
又∵∠1+∠2=90°(已知)
∴
∴
考点:平行线的判定
专题:推理填空题
分析:由条件可得到∠1+∠2=90°,再结合条件和角平分线的定义可求得∠ABC+∠DCB=180°,可得到AB∥CD,据此填空即可.
解答: 解:∵BE平分∠ABC(已知)
解:∵BE平分∠ABC(已知)
∴∠ABC=2∠1( 角平分线的定义 )
∵CE平分∠BCD(已知)
∴∠DCB=2∠2( 角平分线的定义 )
∴∠ABC+∠DCB=2(∠1+∠2).
又∵∠1+∠2=90°(已知)
∴∠ABC+∠DCB=2×90°=180°
∴AB∥CD( 同旁内角互补,两直线平行 ),
故答案为:∠ABC;角平分线的定义;∠DCB;角平分线的定义;∠ABC;∠DCB;∠ABC;∠DCB;AB;CD;同旁内角互补,两直线平行.
 解:∵BE平分∠ABC(已知)
解:∵BE平分∠ABC(已知)∴∠ABC=2∠1( 角平分线的定义 )
∵CE平分∠BCD(已知)
∴∠DCB=2∠2( 角平分线的定义 )
∴∠ABC+∠DCB=2(∠1+∠2).
又∵∠1+∠2=90°(已知)
∴∠ABC+∠DCB=2×90°=180°
∴AB∥CD( 同旁内角互补,两直线平行 ),
故答案为:∠ABC;角平分线的定义;∠DCB;角平分线的定义;∠ABC;∠DCB;∠ABC;∠DCB;AB;CD;同旁内角互补,两直线平行.
点评:本题主要考查平行线的判定和性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
某反比例函数的图象过点(1,-4),则此反比例函数解析式为( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
若4a-9与3a-5互为相反数,则a2-2a+1的值为( )
| A、1 | B、-1 | C、2 | D、0 |