题目内容

直线l的解析式y= $数学公式$ +8，与x轴、y轴分别交于A、B两点，P是x轴上一点，以P为圆心的圆与直线l相切于B点．
（1）求点P的坐标及⊙P的半径R；
（2）若⊙P以每秒 $数学公式$ 个单位沿x轴向左运动，同时⊙P的半径以每秒 $数学公式$ 个单位变小，设⊙P的运动时间是t秒，且⊙P始终与直线l有交点，试求t的取值范围；
（3）在（2）中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值．

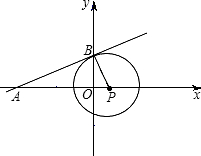解：（1）如图，由于直线l：y= $\text{[math]}$ +8与x轴、y轴分别交于A、B两点，所以A、B两点的坐标可以求出，线段OA、OB的长度也可以求出，又OB⊥AP，AB切⊙P于B点，可以得到△ABO∽△BPO，然后根据相似三角形的对应边成比例就可以求出OP，BP，也就求出了题目的结论；
求得P点坐标（6，0），半径PB=10．

（2）若⊙P以每秒 $\text{[math]}$ 个单位沿x轴向左运动，同时⊙P的半径以每秒 $\text{[math]}$ 个单位变小，
设⊙P的运动时间为t秒，且⊙P始终与直线l有交点，试求t的取值范围；
R≥点P到直线L的距离，则⊙P始终与直线l有交点．
P[（6- $\text{[math]}$ t），0]，R=10- $\text{[math]}$ t，L：3x-4y+32=0
点P到直线L的距离H=|10-2t|
10- $\text{[math]}$ t≥|10-2t|
10- $\text{[math]}$ t≥10-2t≥-（10- $\text{[math]}$ t）
解得：0≤t≤ $\text{[math]}$ ；

（3）在（2）中，设⊙P被直线l截得的弦长为a，问是否存在t的值，使a最大？若存在，求出t的值
一定存在t的值，使a最大
（ $\text{[math]}$ ）²=R²-H²=（10- $\text{[math]}$ t）²-（10-2t）²=（- $\text{[math]}$ ）•（t- $\text{[math]}$ ）²+50
则a²=-7t²+40t，
t= 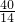$\text{[math]}$ = $\text{[math]}$ 时，a²_最大= $\text{[math]}$ ，a_最大= $\text{[math]}$ ．
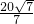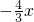分析：（1）直线l的解析式y= $\text{[math]}$ +8，与x轴、y轴分别交于A、B两点，求出A（- $\text{[math]}$ ，0），B（0，8），由圆P与直线l相切的直线PB的解析式y= $\text{[math]}$ +8，求得P点坐标（6，0），PB=10，
（2）由R≥点P到直线L的距离，则⊙P始终与直线l有交点，求得t的取值范围．
（3）先假设存在这样的t，然后由条件求出t值．
点评：此题把一次函数与圆相结合，考查了同学们综合运用所学知识的能力，是一道综合性较好的题目．