题目内容
已知关于x的一元二次方程mx2-(m+2)x+2=有两个不相等的实数根x1,x2.
(1)求m的取值范围;
(2)若x2<0,且
>-1,求整数m的值.
(1)求m的取值范围;
(2)若x2<0,且
| x1 |
| x2 |
考点:根的判别式,根与系数的关系
专题:计算题
分析:(1)由二次项系数不为0,且根的判别式大于0,求出m的范围即可;
(2)利用求根公式表示出方程的解,根据题意确定出m的范围,找出整数m的值即可.
(2)利用求根公式表示出方程的解,根据题意确定出m的范围,找出整数m的值即可.
解答:解:(1)由已知得:m≠0且△=(m+2)2-8m=(m-2)2>0,
则m的范围为m≠0且m≠2;
(2)方程解得:x=
,即x=1或x=
,
∵x2<0,∴x2=
<0,即m<0,
∵
>-1,
∴
>-1,即m>-2,
∵m≠0且m≠2,
∴-2<m<0,
∵m为整数,
∴m=-1.
则m的范围为m≠0且m≠2;
(2)方程解得:x=
| (m+2)±(m-2) |
| 2m |
| 2 |
| m |
∵x2<0,∴x2=
| 2 |
| m |
∵
| x1 |
| x2 |
∴
| m |
| 2 |
∵m≠0且m≠2,
∴-2<m<0,
∵m为整数,
∴m=-1.
点评:此题考查了根的判别式,一元二次方程有两个不相等的实数根即为根的判别式大于0.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列数轴画正确的是( )
A、 |
B、 |
C、 |
D、 |
一客轮船长江从A港顺流到达B港需6小时,从B港逆流到A港需8小时,一天,客轮从A港出发开往B港,2小时后,客轮上的一位旅客的帽子不慎落入江中,则帽子漂流到B港需要( )小时.
| A、48 | B、32 | C、28 | D、24 |
下列结论中,有( )个是错误的.
①-a<0 ②-a<a ③-a≠a ④-a≠0.
①-a<0 ②-a<a ③-a≠a ④-a≠0.
| A、4 | B、3 | C、2 | D、1 |
 如图,⊙O的直径AB垂直于弦CD,垂足是E,OC=5,CD=8,则OE的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,OC=5,CD=8,则OE的长为( )| A、1 | B、2 | C、3 | D、4 |
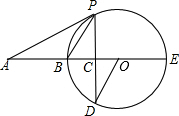 如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.