题目内容
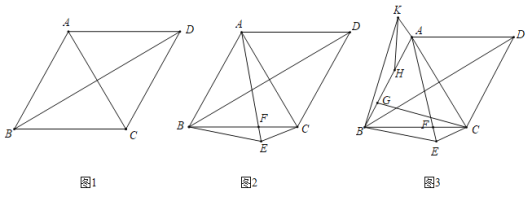
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
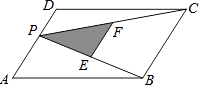
(1)如下图,求证:四边形![]() 是菱形;
是菱形;
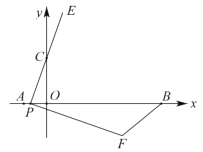
(2)如下图,点![]() 为四边形
为四边形![]() 外一点,连接
外一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
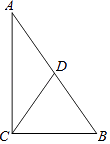
(3)如下图,在(2)的条件下,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见详解;(2)见详解;(3)6![]() .
.
【解析】
(1)首先证明AB=BC,AB=AD,推出AD=BC,可证四边形ABCD是平行四边形即可解决问题.
(2)欲证明AE=AC,只要证明∠ACE=∠AEC即可.
(3)如图3中,作KJ⊥BA交BA的延长线于J,CI⊥AB于I,设BD交AC于O.首先证明△ABC是等边三角形,易知BO⊥AC,CJ⊥AB,推出BO=CJ,因为S△BCG=![]() BGCI,S△ABK=
BGCI,S△ABK=![]() AKBO,由BG=AK,CI=BO,推出S△BCG=S△ABK,推出S△BCG-S△AKH=S△ABK-S△AKH=S△BHK=
AKBO,由BG=AK,CI=BO,推出S△BCG=S△ABK,推出S△BCG-S△AKH=S△ABK-S△AKH=S△BHK=![]() BHKJ,再证明JK=
BHKJ,再证明JK=![]() AK=
AK=![]() BG即可解决问题.
BG即可解决问题.
(1)证明:如图1中,
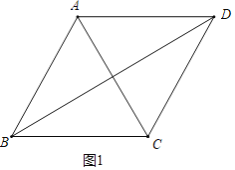
∵AC平分∠BAD,
∴∠CAB=∠CAD,
∵AD∥BC,
∴∠CAD=∠ACB,∠ADB=∠DBC,
∴∠CAB=∠ACB,
∴AB=CB,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形.
(2)证明:如图2中,
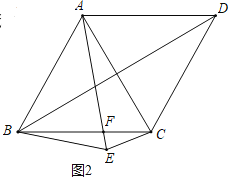
∵BA=BC,
∴∠BAC=∠BCA,
∵∠AFC=2∠AEC-∠BAC,
∴∠AFC+∠ACB=2∠AEC,
∵∠CAF+∠AFC+∠ACB=180°,∠CAE+∠AEC+∠ACE=180°,
∴∠AFC+∠ACB=∠AEC+∠ACE=2∠AEC,
∴∠ACE=∠AEC,
∴AE=AC.
(3)解:如图3中,作KJ⊥BA交BA水电延长线于J,CI⊥AB于I,设BD交AC于O.
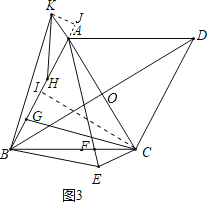
∵AB=AE=AC,
∴△BCE的外接圆的圆心为A,
∵∠BEC=150°,
∴∠EBC+∠BCE=30°,
∵∠EAC=2∠EBC,∠EAB=2∠BCE,
∴∠BAC=2(∠EBC+∠BCE)=60°,
∵BA=BC,
∴△ABC是等边三角形,BO⊥AC,CJ⊥AB,
∴BO=CJ,
∵S△BCG=![]() BGCI,S△ABK=
BGCI,S△ABK=![]() AKBO,
AKBO,
∵BG=AK,CI=BO,
∴S△BCG=S△ABK,
∴S△BCG-S△AKH=S△ABK-S△AKH=S△BHK=![]() BHKJ,
BHKJ,
在Rt△AKJ中,∵∠KAJ=∠BAC=60°,
∴KJ=AKsin60°=![]() AK=
AK=![]() BG,
BG,
∴S△BCG-S△AKH=![]() BHKJ=
BHKJ=![]() BH
BH![]() BG=
BG=![]() BHBG=
BHBG=![]() ×24=6
×24=6![]() .
.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案