Question

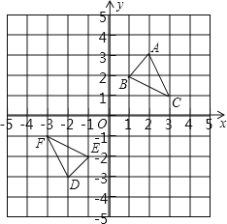
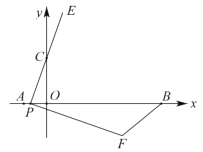
【题目】如图，在平面直角坐标系中，已知点、、的坐标分别为，，．若点从点出发，沿轴正方向以每秒1个单位长度的速度向点移动，连接并延长到点，使，将线段绕点顺时针旋转得到线段，连接．若点在移动的过程中，使成为直角三角形，则点的坐标是__________．

Answer 1

【答案】（5，2），（1）

【解析】

当P位于线段OA上时，显然△PFB不可能是直角三角形；由于∠BPF＜∠CPF=90°，所以P不可能是直角顶点，可分两种情况进行讨论：
①F为直角顶点，过F作FD⊥x轴于D，BP=6-t，DP=2OC=4，在Rt△OCP中，OP=t-1，由勾股定理易求得CP=t2-2t+5，那么PF2=（2CP）2=4（t2-2t+5）；在Rt△PFB中，FD⊥PB，由射影定理可求得PB=PF2÷PD=t2-2t+5，而PB的另一个表达式为：PB=6-t，联立两式可得t2-2t+5=6-t，即t= ；
②B为直角顶点，得到△PFB∽△CPO，且相似比为2，那么BP=2OC=4，即OP=OB-BP=1，此时t=2．

解：能；
①若F为直角顶点，过F作FD⊥x轴于D，则BP=6-t，DP=2OC=4，

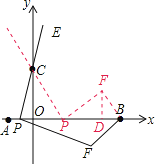
在Rt△OCP中，OP=t-1，
由勾股定理易求得CP2=t2-2t+5，那
么PF2=（2CP）2=4（t2-2t+5）；
在Rt△PFB中，FD⊥PB，
由射影定理可求得PB=PF2÷PD=t2-2t+5，
而PB的另一个表达式为：PB=6-t，
联立两式可得t2-2t+5=6-t，即t=，
P点坐标为（，0），
则F点坐标为：（ 1）；
②B为直角顶点，得到△PFB∽△CPO，且相似比为2，
那么BP=2OC=4，即OP=OB-BP=1，此时t=2，
P点坐标为（1，0）．FD=2（t-1）=2，
则F点坐标为（5，2）．
故答案是：（5，2），（1）．