Question

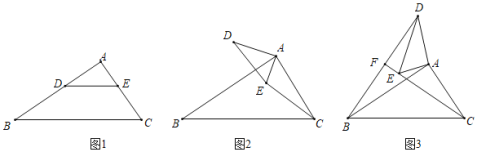
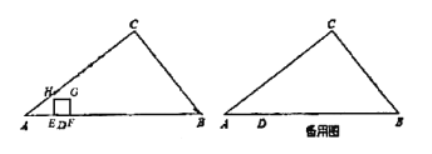
【题目】如图，AB为圆O的直径，C为圆O上的一点，D为BA延长线上的一点，，线段DF分别交AC，BC于点E，F，且=45°，圆O的半径为5，，则CF的长（ ）

A.B.3C.D.4

Answer 1

【答案】A

【解析】

先根据三角函数计算AC=6，BC=8，证明△CAD∽△BCD，得，证明△CED∽△BFD，列比例式可得CF的长．

∵AB为圆O的直径

∴∠BCA=90°

∵AB=2r=10，

设AC=3x，BC=4x，则AB=5x=10

∴x=2
∴AC=6，BC=8，
∵∠ACD=∠B，∠ADC=∠CDB，
∴△CAD∽△BCD，
∴

∵∠CEF=45°，∠ACB=90°，
∴∠CFE=45°，CE=CF，
设CF=CE=a，
∵∠CEF=∠ACD+∠CDE，
∠CFE=∠B+∠BDF，
∴∠CDE=∠BDF，
又∵∠ACD=∠B，
∴△CED∽△BFD，
∴，即

解得：

故选：A