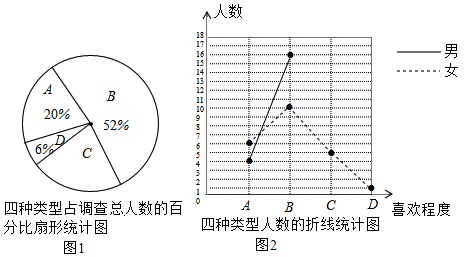
题目内容
7.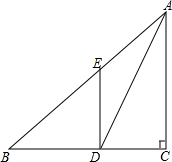 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点E在AB上,DE∥AC,CD=12,BD=15,求AE、BE的长.
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点E在AB上,DE∥AC,CD=12,BD=15,求AE、BE的长.
分析 利用已知条件易证AE=DE,因为DE∥AC,所以可得到BE和AE的关系,即BE和DE的关系,设AE=4x,根据勾股定理可得BE2=DE2+BD2,求出x的值,进而得到AE,BE的长.
解答 解:∵AD平分∠BAC,
∴∠CAD=∠DAE,
∵DE∥CA,
∴∠DAE=∠ADE,
∴AE=DE,
∵DE∥CA,
∴AE:BE=CD:BD=12:15=4:5,
设AE=4x,
则DE=4x,BE=5x,
∵AC⊥BC,DE∥CA,
∴DE⊥BD,
由勾股定理得BE2=DE2+BD2,
所以25x2=16x2+225,
解得x=5,
∴AE=4×5=20,BE=5×5=25.
点评 本题考查了等腰三角形的判定和性质、平行线的性质以及勾股定理的运用,利用平行线分线段成比例定理得到AE和BE的数量关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一元二次方程x2-4x-m=0总有实数根,则m应满足的条件是( )
| A. | m>-4 | B. | m=-4 | C. | m≤-4 | D. | m≥-4 |
15.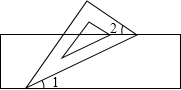 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )| A. | 23° | B. | 27° | C. | 30° | D. | 37° |