题目内容
探索与思考
观察下列等式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?答:
(2)试一试:13+23+33+43+…+93= .
(3)猜一猜:13+23+33+43+…+n3= .
观察下列等式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?答:
(2)试一试:13+23+33+43+…+93=
(3)猜一猜:13+23+33+43+…+n3=
考点:规律型:数字的变化类
专题:
分析:(1)通过观察和计算可知左边各项幂的底数的和等于右边幂的底数;
(2)利用(1)中的结论即可得出规律并求得此式的值;
(3)根据(1)中的观察,用式子表示即可.
(2)利用(1)中的结论即可得出规律并求得此式的值;
(3)根据(1)中的观察,用式子表示即可.
解答:解:(1)等式左边各项幂的底数和等于右边幂的底数;
(2)13+23+…+93=(1+2+…+9)2=
×92×102=2025;
(3)(1+2+3+…+n)2或
n2(n+1)2.
故答案为:等式左边各项幂的底数和等于右边幂的底数;2025;
n2(n+1)2.
(2)13+23+…+93=(1+2+…+9)2=
| 1 |
| 4 |
(3)(1+2+3+…+n)2或
| 1 |
| 4 |
故答案为:等式左边各项幂的底数和等于右边幂的底数;2025;
| 1 |
| 4 |
点评:此题主要考查了数字的变化规律,找等式的规律时,要注意观察等式的左边和右边的规律,还要注意观察等式的左右两边之间的关系.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
如图1是玩具拼图模板的一部分,已知△ABC的六个元素,则图2中甲、乙、丙三个三角形中能和△ABC完全重合的是( )
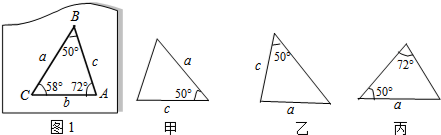
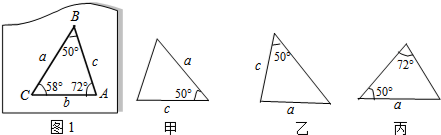
| A、甲和丙 | B、丙和乙 |
| C、只有甲 | D、只有丙 |
大于-4.2且小于3.8的整数有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
函数y=-x2-4x+3图象顶点坐标是( )
| A、(2,-7) |
| B、(2,7) |
| C、(-2,-7) |
| D、(-2,7) |
 一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是1米,测得OC⊥AB,垂足为C,且OC=0.3米,则水平面宽AB=
一根水平面放置的圆柱形排水管横截面如图所示,已知排水管道的直径是1米,测得OC⊥AB,垂足为C,且OC=0.3米,则水平面宽AB= 如图一次函数y=kx+b的图象经过点A和点B.
如图一次函数y=kx+b的图象经过点A和点B.