题目内容
已知k=| a+b-c |
| c |
| a-b+c |
| b |
| -a+b+c |
| a |
| m+6 |
分析:可分a+b+c=0和a+b+c≠0两种情况代入求值和利用等比性质求得k可能的值,把含m,n的等式整理为两个非负数的和的形式,即可得到m,n准确的值,进而根据一次函数图象的性质得到一定经过的象限.
解答:解:n2+16+
=8n,
n2-8n+16+
=0,
(n-4)2+
=0,
∴n-4=0,m+6=0,
解得n=4,m=-6.
∴n-m=10.
①a+b+c=0时,
a+b=-c,
∴k=
=
=-2,
∴-k=2,
此时一次函数经过一、二、三象限;
②a+b+c≠0时,
k=
=
=1,
∴-k=-1,
此时一次函数经过一、二、四象限;
∴关于x的一次函数y=-kx+n-m的图象一定经过第一、二象限,
故答案为一、二.
| m+6 |
n2-8n+16+
| m+6 |
(n-4)2+
| m+6 |
∴n-4=0,m+6=0,
解得n=4,m=-6.
∴n-m=10.
①a+b+c=0时,
a+b=-c,
∴k=
| a+b-c |
| c |
| -2c |
| c |
∴-k=2,
此时一次函数经过一、二、三象限;
②a+b+c≠0时,
k=
| a+b-c+a-b+c-a+b+c |
| c+b+a |
| a+b+c |
| c+b+a |
∴-k=-1,
此时一次函数经过一、二、四象限;
∴关于x的一次函数y=-kx+n-m的图象一定经过第一、二象限,
故答案为一、二.
点评:考查比例性质的应用及一次函数图象的性质;分类探讨出t可能的值是解决本题的突破点;用到的知识点为:一次函数的比例系数,常数项均大于0,图象经过一、二、三象限;一次函数的比例系数,常数项均小于0,图象经过二、三、四象限;

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
已知k=
=
=
,且
+n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.
| a+b-c |
| c |
| a-b+c |
| b |
| -a+b+c |
| a |
| m-5 |
| A、一、二 | B、二、三 |
| C、三、四 | D、一、四 |
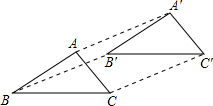 如图,△A′B′C′是由△ABC平移而得到的.已知AB=6,CC′=12,∠BAC=95°,∠ACB=45°,则∠A′B′C′=
如图,△A′B′C′是由△ABC平移而得到的.已知AB=6,CC′=12,∠BAC=95°,∠ACB=45°,则∠A′B′C′=