题目内容
5. 如图,⊙O 的半径为1,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,若∠APB=60°,则△PAB的周长为3$\sqrt{3}$.
如图,⊙O 的半径为1,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,若∠APB=60°,则△PAB的周长为3$\sqrt{3}$.
分析 根据切线的性质得到OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,推出△PAB是等边三角形,根据直角三角形的性质得到PA=$\sqrt{3}$AO=$\sqrt{3}$,于是得到结论.
解答 解:∵PA、PB是半径为1的⊙O的两条切线,
∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,
而∠APB=60°,
∴∠APO=30°,△PAB是等边三角形,
∴PA=$\sqrt{3}$AO=$\sqrt{3}$,
∴△PAB的周长=$3\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查了切线的性质,直角三角形的性质,三角形的周长的计算,熟练掌握切线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如图:
小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如图:
调查问卷你最喜欢的球类运动是D(单选)
A.篮球 B.足球 C.排球 D.乒乓球 E.羽毛球 F.其他
小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如下:
(1)请你写出统计表的空缺部分的人数m=63,n=96;
(2)在扇形统计图中,羽毛球所对应扇形的圆心角等于115.2°;
(3)请你根据调查结果,给小强部长简要提出合理化的建议.
 小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如图:
小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如图:调查问卷你最喜欢的球类运动是D(单选)
A.篮球 B.足球 C.排球 D.乒乓球 E.羽毛球 F.其他
小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如下:
| 组别 | 篮球 | 足球 | 排球 | 乒乓球 | 羽毛球 | 其他 |
| 人数 | 69 | m | 27 | n | 36 | 9 |
(2)在扇形统计图中,羽毛球所对应扇形的圆心角等于115.2°;
(3)请你根据调查结果,给小强部长简要提出合理化的建议.
13.1纳米=10-9米,甲型H1N1病毒细胞的直径约为156纳米,则156纳米写成科学记数法的形式是( )
| A. | 156×10-9米 | B. | 15.6×10-8米 | C. | 1.56×10-7米 | D. | 0.156×10-7米 |
 如图,点B,D,C,F在同一条直线上,∠A=∠E,AB=EF,∠B=∠F.求证:BD=CF.
如图,点B,D,C,F在同一条直线上,∠A=∠E,AB=EF,∠B=∠F.求证:BD=CF.
 如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,$\sqrt{3}$≈1.73
如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,$\sqrt{3}$≈1.73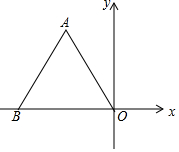 如图,ABO是边长为3 的等边三角形,则A点的坐标是(-$\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$)..
如图,ABO是边长为3 的等边三角形,则A点的坐标是(-$\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$)..