题目内容
如图，AD为△ABC的角平分线，BE⊥AD的延长线于E，CF⊥AD于F，BF、EC的延长线交于点P，求证：CF∥AP．考点：相似三角形的判定与性质
专题：证明题
分析：由条件可得CF∥BE，结合条件可证明△BAE∽△ACF，可得到
=
，则有CF∥AP．
| CP |
| PE |
| AF |
| AE |
解答：证明：∵CF⊥AE，BE⊥AE，
∴CF∥BE，
∴
=
，
∴∠AFC=∠AEB=90°，
∵AD是∠BAC的平分线，
∴∠BAE=∠EAC，
∴△BAE∽△ACF，
∴
=
，
∴
=
，
∴CF∥AP．
∴CF∥BE，
∴
| CP |
| PE |
| CF |
| BE |
∴∠AFC=∠AEB=90°，
∵AD是∠BAC的平分线，
∴∠BAE=∠EAC，
∴△BAE∽△ACF，
∴
| AF |
| AE |
| CF |
| BE |
∴
| CP |
| PE |
| AF |
| AE |
∴CF∥AP．
点评：本题主要考查平行线分线段成比例的逆定理及相似三角形的判定及性质，掌握相似三角形的对应边成比例是解题的关键，注意由线段对应成比例也可以证明平行．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
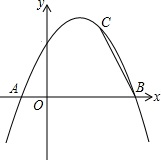如图，抛物线y=-
在?ABCD中，对角线AC、BD相交于O，AE⊥BC，垂足为E，EO的延长线交AD于点F，请你观察猜想四边形AECF的形状，并说明理由．