题目内容
已知直线![]() 与
与![]() 轴
轴![]() 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)
(1)求的![]() 值和点A的坐标;
值和点A的坐标;
(2)在矩形OACB中,点P是线段BC上的一动点,直线PD⊥AB于点D,与![]() 轴交于点E,设BP=
轴交于点E,设BP=![]() ,梯形PEAC的面积为
,梯形PEAC的面积为![]() 。
。
①求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②⊙Q是△OAB的内切圆,求当PE与⊙Q相交的弦长为2.4时点P的坐标。

解:(1)把B(0,6)代入![]() ,得
,得![]() =6…
=6…
把![]() =0代入
=0代入![]() ,得
,得![]() =8
=8
∴点A的坐标为(8,0)
(2)在矩形OACB中,AC=OB=6,
BC=OA=8,∠C=90°
∴AB=![]()
 ∵PD⊥AB
∵PD⊥AB
∴∠PDB=∠C=90°
![]()
∴![]()
∴![]()
∴![]()
又∵BC∥AE
∴△PBD∽△EAD
∴![]() ,即
,即
∴![]()
∵![]()
∴![]() (
(![]() )
)
(注:写成![]() 不扣分)
不扣分)
② ⊙Q是△OAB的内切圆 ,可设⊙Q的半径为r
∵![]()
![]() ,解得r=2.
,解得r=2.
设⊙Q与OB、AB、OA分别切于点F、G、H
可知,OF=2
∴BF=BG=OB-OF=6-2=4
设直线PD与⊙Q交于点 I、J ,过Q作QM⊥IJ于点M,连结IQ、QG
∵QI=2,![]()
∴ ![]()
∴ 在矩形GQMD中,GD=QM=1.6
∴BD=BG+GD=4+1.6=5.6
由![]()
得![]()
∴点P的坐标为(7,6)
当PE在圆心Q的另一侧时,同理可求点P的坐标为(3,6)
综上,P点的坐标为(7,6)或(3,6)。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
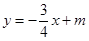 与
与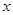 轴
轴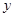 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)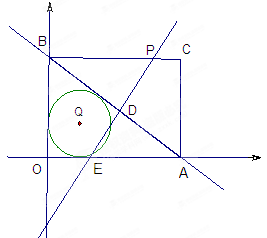
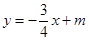 与
与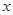 轴
轴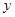 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)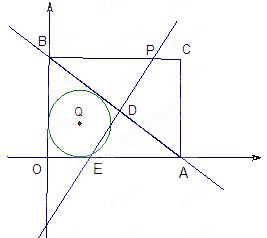
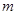 值和点A的坐标;
值和点A的坐标;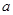 ,梯形PEAC的面积为
,梯形PEAC的面积为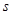 。
。 与
与 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6) 值和点A的坐标;
值和点A的坐标; 与t的函数关系式;
与t的函数关系式;
 与
与 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6) 值和点A的坐标;
值和点A的坐标; 与t的函数关系式;
与t的函数关系式;
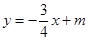 与
与 轴
轴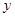 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)
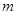 值和点A的坐标;
值和点A的坐标;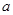 ,梯形PEAC的面积为
,梯形PEAC的面积为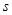 。
。