题目内容
已知直线 与
与 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)【小题1】求的
 值和点A的坐标;
值和点A的坐标;【小题2】在矩形OACB中,某动点P从点B出发以每秒1个单位的速度沿折线B-C-A运动.运动至点A停止.直线PD⊥AB于点D,与
 轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.①求
 与t的函数关系式;
与t的函数关系式;②⊙Q是△OAB的内切圆,问:t为何值时,PE与⊙Q相交的弦长为2.4 ?

【小题1】
 =6
=6【小题1】见解析解析:
【小题1】解:把B(0,6)代入
 ,得
,得 =6
=6把
 =0代入
=0代入 ,得
,得 =8
=8∴点A的坐标为(8,0)…
【小题1】在矩形OACB中,AC=OB=6,
BC=OA=8,∠C=90°
∴AB=

当
 时,
时,
当
 时
时∵BC∥AE
由△PBD∽△EAD
求得

∵

∴

当


② ⊙Q是△OAB的内切圆 ,可设⊙Q的半径为r
∵

 ,解得r=2.
,解得r=2.设⊙Q与OB、AB、OA分别切于点F、G、H
可知,OF=2
∴BF=BG=OB-OF=6-2=4…………
设直线PD与⊙Q交于点 I、J ,过Q作QM⊥IJ于点M,连结IQ、QG
∵QI=2,

∴

∴ 在矩形GQMD中,GD=QM=1.6
∴BD=BG+GD=4+1.6=5.6
由

得
 ∴t=7
∴t=7 当PE在圆心Q的另一侧时,同理可求t=3 综上,t=7 或t=3


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
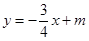 与
与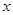 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)
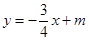 与
与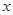 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)
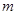 值和点A的坐标;
值和点A的坐标;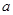 ,梯形PEAC的面积为
,梯形PEAC的面积为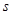 。
。 与
与 轴
轴 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6) 值和点A的坐标;
值和点A的坐标; 与t的函数关系式;
与t的函数关系式;
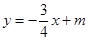 与
与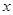 轴
轴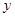 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)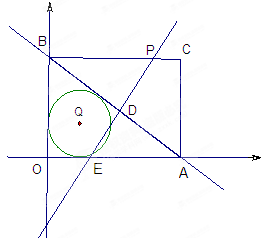
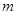 值和点A的坐标;
值和点A的坐标;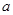 ,梯形PEAC的面积为
,梯形PEAC的面积为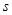 。
。