题目内容
15.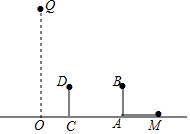 如图,身高1.6米的小明站在距路灯底部O点10米的点A处,他的身高(线段AB)在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
如图,身高1.6米的小明站在距路灯底部O点10米的点A处,他的身高(线段AB)在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.(1)在OQ上画出表示路灯灯泡位置的点P;
(2)小明沿AO方向前进到点C,请画出此时表示小明影子的线段CN;
(3)若AM=2.5米,求路灯灯泡P到地面的距离.
分析 (1)MB的延长线与OQ的交点为P;
(2)连接PD并延长交路面于点N;
(3)利用相似三角形对应边成比例列式列式即可得解.
解答 解:(1)如图:
(2)如图:
(3)∵AB∥OP,
∴△MAB∽△MOP,
∴$\frac{AB}{OP}$=$\frac{AM}{OM}$,即$\frac{1.6}{OP}$=$\frac{2.5}{10+2.5}$,
解得OP=8.
即路灯灯泡P到地面的距离是8米.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列计算正确的是( )
| A. | 4x-9x+6x=-x | B. | a-a=0 | C. | x3-x2=x | D. | xy-2xy=3xy |
10.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (b-a)2=b2-2ab+a2 | C. | (a+2b)(a-2b)=a2-2b2 | D. | (a-b)2=a2-2ab-b2 |
4.国庆期间,某公园门票规定如下表:
某校七年级(1)(2)两个班共104人去游园,如果以班为单位购票,共付1240元,其中(1)班人数大于40人小于50人,试问:
(1)这两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票最省钱?
| 购票人数 | 1-50张 | 51~100张 | 100张以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)这两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票最省钱?
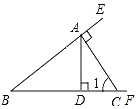 如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:
如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:
 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为3cm.
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为3cm. 如图,数轴上点A、B、C所对应的数分别为a、b、c,化简|a|+|c-b|-|a+b-c|=0.
如图,数轴上点A、B、C所对应的数分别为a、b、c,化简|a|+|c-b|-|a+b-c|=0.