题目内容
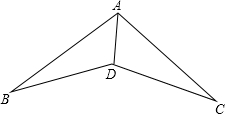 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A、BD=DC,AB=AC |
| B、∠B=∠C,BD=CD |
| C、∠ADB=∠ADC,BD=DC |
| D、∠B=∠C,∠BAD=∠CAD |
考点:全等三角形的判定
专题:
分析:根据全等三角形的判定方法SSS、SAS、ASA、AAS分别进行分析即可.
解答:解:A、BD=DC,AB=AC,再加公共边AD=AD可利用SSS定理进行判定,故此选项不合题意;
B、∠B=∠C,BD=CD,再加公共边AD=AD不能判定△ABD≌△ACD,故此选项符合题意;
C、∠ADB=∠ADC,BD=DC再加公共边AD=AD可利用SAS定理进行判定,故此选项不合题意;
D、∠B=∠C,∠BAD=∠CAD再加公共边AD=AD可利用AAS定理进行判定,故此选项不合题意;
故选:B.
B、∠B=∠C,BD=CD,再加公共边AD=AD不能判定△ABD≌△ACD,故此选项符合题意;
C、∠ADB=∠ADC,BD=DC再加公共边AD=AD可利用SAS定理进行判定,故此选项不合题意;
D、∠B=∠C,∠BAD=∠CAD再加公共边AD=AD可利用AAS定理进行判定,故此选项不合题意;
故选:B.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
如果四条线段a,b,c,d构成
=
,m>0,则下面推理正确的有( )
①
=
;②
=
;③
=
;④
=
.
| a |
| b |
| c |
| d |
①
| a |
| b |
| cm |
| dm |
| a |
| b |
| 7a+cm |
| 7b+dm |
| a |
| b |
| c+m |
| d+m |
| a |
| a+cm |
| b |
| b+dm |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法正确的是( )
| A、一个数与其倒数之商为-1 | ||
B、a的倒数是
| ||
| C、a的相反数是-a | ||
| D、2a>a(a为有理数) |
已知抛物线y=5(x-1)2,下列说法中,你认为不正确的是( )
| A、顶点坐标为(1,0) |
| B、对称轴为直线x=0 |
| C、当x>1时,y随x的增大而增大 |
| D、当x<1时,y随x的增大而减小 |
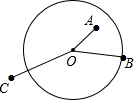 如图,设⊙O的半径为r,A点在圆内,OA
如图,设⊙O的半径为r,A点在圆内,OA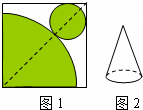 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为1,扇形的圆心角等于90°,则扇形的半径是( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为1,扇形的圆心角等于90°,则扇形的半径是( )