题目内容
9.已知一元二次方程x2+bx+c=0的两个实数根为-1,3,则b=-2,c=-3.分析 利用根与系数的关系可求得b与c的值.
解答 解:由根与系数的关系可知x1+x2=-b=-1+3,
即b=-2,
x1•x2=c=-1×3=-3,
即c=-3.
故答案为:-2,-3.
点评 本题考查了一元二次方程根与系数的关系.解题关键是会利用根与系数的关系来求方程中的字母系数.一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
19.现规定一种新的运算符号“※”:a※b=ab,如3※2=32,则$\frac{1}{2}$※3=( )
| A. | $\frac{1}{8}$ | B. | 8 | C. | $\frac{1}{6}$ | D. | $\frac{3}{2}$ |
 已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.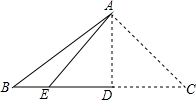 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2-AC2的值为( )
如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2-AC2的值为( )