Question

19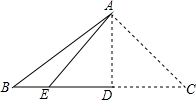．如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处．若BC=8，BE=2．则AB²-AC²的值为（　　）

• A． 4
• B． 6
• C． 10
• D． 16

Answer 1

分析 根据折叠的性质得到AE=AC，DE=CD，AD⊥BC，由勾股定理得到AB²=AD²+BD²，AC²=AD²+CD²，两式相减，通过整式的化简即可得到结论．

解答 解：∵将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处，
∴AE=AC，DE=CD，AD⊥BC，
∴AB²=AD²+BD²，AC²=AD²+CD²，
∴AB²-AC²=AD²+BD²-AD²-CD²=BD²-CD²=（BD+CD）（BD-CD）=BC•BE，
∵BC=8，BE=2，
∴AB²-AC²=8×2=16．
故选D．

点评 本题考查了翻折变换-折叠问题，勾股定理，整式的化简，熟练掌握折叠的性质是解题的关键．