Question

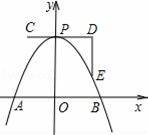
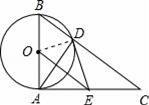
如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．

（1）求证：ED是⊙O的切线．

（2）当OA=3，AE=4时，求BC的长度．

　

Answer 1

【考点】切线的判定；垂径定理．

【专题】几何综合题．

【分析】（1）如图，连接OD．通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°，易证得结论；

（2）利用圆周角定理和垂径定理推知OE∥BC，所以根据平行线分线段成比例求得BC的长度即可．

【解答】（1）证明：如图，连接OD．

∵AC⊥AB，

∴∠BAC=90°，即∠OAE=90°．

在△AOE与△DOE中，

，

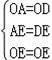
∴△AOE≌△DOE（SSS），

∴∠OAE=∠ODE=90°，即OD⊥ED．

又∵OD是⊙O的半径，

∴ED是⊙O的切线；

（2）解：如图，在△OAE中，∠OAE=90°，OA=3，AE=4，

∴由勾股定理易求OE=5．

∵AB是直径，

∴∠ADB=90°，即AD⊥BC．

又∵由（1）知，△AOE≌△DOE，

∴∠AEO=∠DEO，

又∵AE=DE，

∴OE⊥AD，

∴OE∥BC，

∴==．

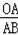
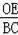
BC=2OE=10，即BC的长度是10．

【点评】本题考查了切线的判定与性质．解答（2）题时，也可以根据三角形中位线定理来求线段BC的长度．