题目内容
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),与
右侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和![]() ,
,![]() 两点的坐标;
两点的坐标;
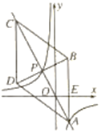
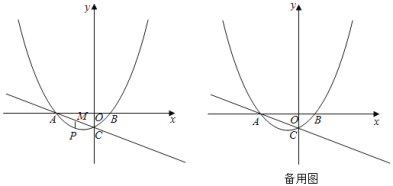
(2)如图1,若点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点之间的一个动点(不与
两点之间的一个动点(不与![]() 、
、![]() 重合),是否存在点
重合),是否存在点![]() ,使四边形
,使四边形![]() 的面积最大?若存在,求点
的面积最大?若存在,求点![]() 的坐标及四边形
的坐标及四边形![]() 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
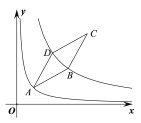
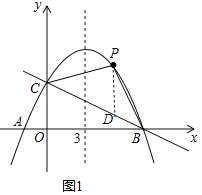
(3)如图2,若点![]() 是抛物线上任意一点,过点
是抛物线上任意一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)存在点
;(2)存在点![]() ,使四边形
,使四边形![]() 的面积最大;点
的面积最大;点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 面积的最大值为32;(3)点
面积的最大值为32;(3)点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由抛物线的对称轴是直线 x=3,解出 a的值,即可求得抛物线解析式,在
令其 y值为零,解一元二次方程即可求出 A和 B的坐标;
(2)易求点 C的坐标为(0,4),设直线 BC的解析式为 y=kx+b(k≠0),将 B(8,0),
C(0,4)代入 y=kx+b,解出 k和 b的值,即得直线 BC的解析式;设点 P的坐标为![]() ,过点 P作 PD∥y轴,交直线 BC于点 D,则点 D的坐标为
,过点 P作 PD∥y轴,交直线 BC于点 D,则点 D的坐标为![]() , 利用关系式 S四边形 PBOC=S△BOC+S△PBC得出关于 x的二次函数,从而求得其最值;
, 利用关系式 S四边形 PBOC=S△BOC+S△PBC得出关于 x的二次函数,从而求得其最值;
(3)设点 M的坐标为![]() 则点 N的坐标为
则点 N的坐标为![]() ,
,![]() ,分当 0<m<8时,或当 m<0或 m> 8时来化简绝对值,从而求解.
,分当 0<m<8时,或当 m<0或 m> 8时来化简绝对值,从而求解.
(1)![]() 抛物线的对称轴是直线
抛物线的对称轴是直线![]() ,
,
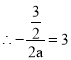 ,解得
,解得![]() ,
,
![]()
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
答:抛物线的解析式为:![]() ;点
;点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2)当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() 得
得
![]() ,解得
,解得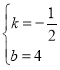 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
假设存在点![]() ,使四边形
,使四边形![]() 的面积最大,
的面积最大,
设点![]() 的坐标为
的坐标为![]() ,如图所示,过点
,如图所示,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,四边形
时,四边形![]() 的面积最大,最大值是32
的面积最大,最大值是32
![]() ,
,
![]() 存在点
存在点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
答:存在点![]() ,使四边形
,使四边形![]() 的面积最大;点
的面积最大;点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 面积的最大值为32.
面积的最大值为32.
(3)设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
当![]() 或
或![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
答:点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案