Question

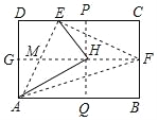
【题目】如图，矩形纸片ABCD中，G、F分别为AD、BC的中点，将纸片折叠，使D点落在GF上，得到△HAE，再过H点折叠纸片，使B点落在直线AB上，折痕为PQ．连接AF、EF，已知HE=HF，下列结论：①△MEH为等边三角形；②AE⊥EF；③△PHE∽△HAE；④ ，其中正确的结论是（　　）

A. ①②③ B. ①②④ C. ①③④ D. ①②③④

Answer 1

【答案】D

【解析】试题解析：∵矩形纸片ABCD中，G、F分别为AD、BC的中点，

∴GF⊥AD，

由折叠可得，AH=AD=2AG，∠AHE=∠D=90°，

∴∠AHG=30°，∠EHM=90°-30°=60°，

∴∠HAG=60°=∠AED=∠MEH，

∴△EHM中，∠EMH=60°=∠EHM=∠MEH，

∴△MEH为等边三角形，故①正确；

∵∠EHM=60°，HE=HF，

∴∠HEF=30°，

∴∠FEM=60°+30°=90°，即AE⊥EF，故②正确；

∵∠PEH=∠MHE=60°=∠HEA，∠EPH=∠EHA=90°，

∴△PHE∽△HAE，故③正确；

设AD=2=AH，则AG=1，

∴Rt△AGH中，GH=AG=，

Rt△AEH中，EH= ，

∴GF==AB，

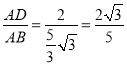∴，故④正确，

综上所述，正确的结论是①②③④，

故选：D．