Question

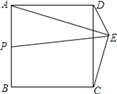
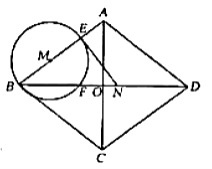
【题目】如图，菱形中，对角线相交于点，，动点从点出发，沿线段以的速度向点运动，同时动点从点出发，沿线段以的速度向点运动，当其中一个动点停止运动时另一个动点也随之停止.设运动时间为，以点为圆心，为半径的⊙与射线，线段分别交于点，连接.

（1）求的长（用含有的代数式表示），并求出的取值范围；

（2）当为何值时，线段与⊙相切？

（3）若⊙与线段只有一个公共点，求的取值范围.

Answer 1

【答案】（1）BF=t（0＜t≤8）．（2）t=s时，线段EN与⊙M相切．（3）当0＜t≤或＜t＜8时，⊙M与线段EN只有一个公共点．

【解析】

试题分析：（1）连接MF．只要证明MF∥AD，可得，即，解方程即可；

（2）当线段EN与⊙M相切时，易知△BEN∽△BOA，可得，即，解方程即可；

（3）①由题意可知：当0＜t≤时，⊙M与线段EN只有一个公共点．②当F与N重合时，则有t+2t=16，解得t=，观察图象即可解决问题

试题解析：（1）连接MF．

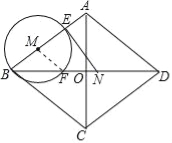
∵四边形ABCD是菱形，

∴AB=AD，AC⊥BD，OA=OC=6，OB=OD=8，

在Rt△AOB中，AB==10，

∵MB=MF，AB=AD，

∴∠ABD=∠ADB=∠MFB，

∴MF∥AD，

∴，

∴，

∴BF=t（0＜t≤8）．

（2）当线段EN与⊙M相切时，易知△BEN∽△BOA，

∴，

∴，

∴t=．

∴t=s时，线段EN与⊙M相切．

（3）①由题意可知：当0＜t≤时，⊙M与线段EN只有一个公共点．

②当F与N重合时，则有t+2t=16，解得t=，

关系图象可知，＜t＜8时，⊙M与线段EN只有一个公共点．

综上所述，当0＜t≤或＜t＜8时，⊙M与线段EN只有一个公共点．