Question

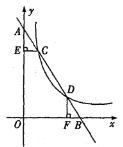
【题目】如图，△AOB中，∠O=90°，AO=8cm，BO=6cm，点C从A点出发，在边AO上以4cm/s的速度向O点运动，与此同时，点D从点B出发，在边BO上以3cm/s的速度向O点运动，过OC的中点E作CD的垂线EF，则当点C运动了________s时，以C点为圆心，2cm为半径的圆与直线EF相切．

Answer 1

【答案】

【解析】

当以点C为圆心，2cm为半径的圆与直线EF相切时，即CF=2cm，又因为∠EFC=∠O=90°，所以△EFC∽△DOC，利用对应边的比相等即可求出EF的长度，再利用勾股定理列出方程即可求出t的值，要注意t的取值范围为0≤t≤2．

当以点C为圆心，2cm为半径的圆与直线EF相切时，

此时，CF=2，

由题意得：AC=4t，BD=3t

∴OC=8-4t，OD=6-3t，

∵点E是OC的中点，

∴CE=OC=4-2t，

∵∠EFC=∠O=90°，∠FCE=∠DCO，

∴△EFC∽△DOC，

∴，

∴EF=，

由勾股定理可知：CE2=CF2+EF2，

∴（4-2t）2=2 2+（）2，

解得：t=或t=，

∵0≤t≤2，

∴t=．

故答案为：．