Question

【题目】若平面内两点P1（x1，y2），P2（x2，y2），其两点间的距离P1P2

例如：已知A（3，1），B（5，2），则这两点间的距离AB．

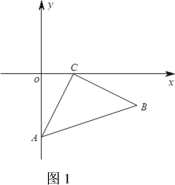
已知A（3，1），B（5，2），C（4，4）

（1）聪明的你能判定ABC的形状吗？并说明理由

（2）若以点A、B、C、D为顶点的四边形是平行四边形时，请直接写出点D的坐标．

Answer 1

【答案】（1）△ABC是等腰直角三角形，理由见解析；（2）D的坐标为（2，3）或（6，5）或（4，－1）

【解析】

（1）根据两点间距离公式求得AB、AC、BC的长度，再根据勾股定理判断△ABC的形状；

（2）分别以AB、BC、AC为对角线时，分别得出D的坐标即可．

（1）△ABC是等腰直角三角形，理由如下：

根据两点间距离公式可得：

∵A（3，1），B（5，2），C（4，4），

∴AB=，AC=，BC=，

∴AB2+BC2＝AC2，AB=BC，

∴△ABC是等腰直角三角形．

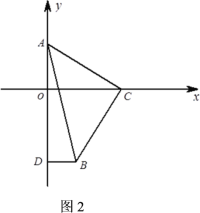
（2）如图所示：

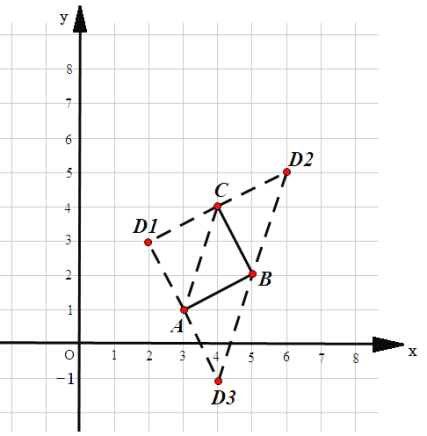
当以AC为对角线时，D的坐标为（2，3）；

当以BC为对角线时，D的坐标为（6，5）；

当以AB为对角线时，D的坐标为（4，－1）；

综上可得，D的坐标为（2，3）或（6，5）或（4，－1）．