题目内容
【题目】在平面直角坐标系中,![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,线段
,线段![]() ,线段
,线段![]() ,且
,且![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,连接
,连接![]() .
.

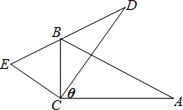
(1)如图1,在线段![]() 上有两个动点
上有两个动点![]() (
(![]() 在
在![]() 上方),且
上方),且![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]()
![]() 的值最小时,求出
的值最小时,求出![]() 的坐标及
的坐标及![]() 的面积.
的面积.
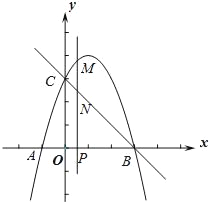
(2)![]() 沿
沿![]() 轴平移,当点
轴平移,当点![]() 平移到
平移到![]() 边上时,平移后的
边上时,平移后的![]() ,在
,在![]() 轴上一动点
轴上一动点![]() ,在平面直角坐标系内有一动点
,在平面直角坐标系内有一动点![]() ,使点
,使点![]() 形成的四边形为菱形,若存在直接写出点
形成的四边形为菱形,若存在直接写出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
【答案】(1)P(![]() ,-3
,-3![]() ),
),![]() 的面积=2
的面积=2![]() ;(2)(12,-2
;(2)(12,-2![]() )或(8,2
)或(8,2![]() )或(8+4
)或(8+4![]() ,-2
,-2![]() )
)
【解析】
(1)先根据直角三角形的性质求出OE=2![]() ,由勾股定理得BE=4
,由勾股定理得BE=4![]() ,得出∠ABE=30°,∠EBC=90°,作点F关于EB的对称点H,过H作HP⊥CD于P,交BE于K,交AB于M,则KH=KF,HP的长即KF+KP 的最小值,此时
,得出∠ABE=30°,∠EBC=90°,作点F关于EB的对称点H,过H作HP⊥CD于P,交BE于K,交AB于M,则KH=KF,HP的长即KF+KP 的最小值,此时![]()
![]() 的值最小,由(
的值最小,由(![]() 在
在![]() 上方),且
上方),且![]() 可得出此时点G于点B重合,根据直角三角形的性质求出HP、HM、HK、MK、MG的长,即可解答本题;
可得出此时点G于点B重合,根据直角三角形的性质求出HP、HM、HK、MK、MG的长,即可解答本题;
(2)![]() 沿
沿![]() 轴平移,当点
轴平移,当点![]() 平移到
平移到![]() 边上时,平移后的
边上时,平移后的![]() 中
中![]() 与B重合,分三种情况:①
与B重合,分三种情况:①![]() 为对角线时,②
为对角线时,②![]() 为对角线时,③
为对角线时,③![]() 为对角线时,分别画出图形,利用菱形的性质,直角三角形的性质等知识一一求解即可.
为对角线时,分别画出图形,利用菱形的性质,直角三角形的性质等知识一一求解即可.
解:(1)由题意得OA=2,则OB=6,
∵![]() ,
,
∴∠AEO=30°,OE=2![]() ,
,
Rt△OBE中,BE=![]() =4
=4![]() ,
,
∴∠ABE=30°,
∵![]() ,
,![]() ,
,
∴∠ABC=180°-∠BAD =120°,∠C=60°,AD=BC=6
∴∠EBC=90°,EB⊥BC,
作点F关于EB的对称点H,过H作HP⊥CD于P,交BE于K,交AB于M,则KH=KF,HP的长即KF+KP 的最小值,此时![]()
![]() 的值最小,
的值最小,

∵ HP⊥CD,∠C=60°
∴∠H=30°
∵点![]() 为
为![]() 中点,BC=6,点F关于EB的对称点H,
中点,BC=6,点F关于EB的对称点H,
∴HG=3,CH=9,
在Rt△CPH,Rt△HBK,Rt△HBM中,
HP=![]() ,
,![]() ,KH=2
,KH=2![]() ,BM=
,BM=![]() ,HM=
,HM=![]() ,
,
∴MP=HP-HM=3![]() ,OM=OB-BM=
,OM=OB-BM=![]() ,MK=HK-HM=
,MK=HK-HM=![]() ,
,
∴P的坐标(![]() ,-3
,-3![]() );
);
∵线段![]() 上有两个动点
上有两个动点![]() (
(![]() 在
在![]() 上方),且
上方),且![]() ,
,![]() ,
,
∴此时点G于点B重合,
∴![]() 的面积=
的面积=![]() AGKM=
AGKM=![]() ×8×
×8×![]() =2
=2![]() ;
;
胡答案为:P(![]() ,-3
,-3![]() ),
),![]() 的面积=2
的面积=2![]() ;
;
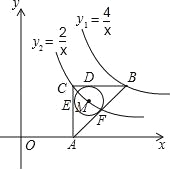
(2)①如图,![]() 为对角线时,作NH⊥AB与H,由题意得A1B1=8,E1B1=4
为对角线时,作NH⊥AB与H,由题意得A1B1=8,E1B1=4![]() ,∠B1A1E1=60°,∠A1B1E1=30°,E1A1=4,
,∠B1A1E1=60°,∠A1B1E1=30°,E1A1=4,

∵菱形![]()
∴∠A1B1N=60°,∠A1ME1=∠MA1E1=60°,
∴ME1= A1E1=B1N=4,
∴HB1=2,HN=2![]() ,
,
∴OH=OB1-HB1=12,
∴点![]() 的坐标(12,-2
的坐标(12,-2![]() );
);
②![]() 为对角线时,
为对角线时,

∵菱形![]()
∴∠E1B1N=60°,NE1=B1E1=4![]() , HE1=HN=2
, HE1=HN=2![]() ,
,
∴HB1=6,
∴OH=OB1-HB1=8,
∴点![]() 的坐标(8,2
的坐标(8,2![]() );
);
![]() 为对角线时,作NH⊥AB与H,
为对角线时,作NH⊥AB与H,

由题意得∠B1MN=30°,MN=B1E1=B1M=4![]() ,
,
∴HM=6,HN=2![]() ,
,
∴B1H=4![]() -6,
-6,
∴OH=OB1+HB1=14+(4![]() -6)=8+4
-6)=8+4![]() ,
,
∴点![]() 的坐标(8+4
的坐标(8+4![]() ,-2
,-2![]() ).
).
故点![]() 的坐标为:(12,-2
的坐标为:(12,-2![]() )或(8,2
)或(8,2![]() )或(8+4
)或(8+4![]() ,-2
,-2![]() ).
).

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案