Question

如图，有一块矩形纸片ABCD，AB=8，AD=6．将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则CF的长为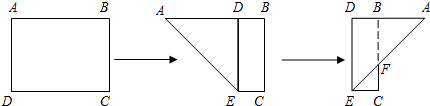

 

．

Answer 1

考点：翻折变换（折叠问题）

专题：

分析：根据已知和折叠得出AD=6，CE=DB=8-6=2，BA=6-2=4，BC=6，根据矩形的性质得出AD∥CE，推出△ABF∽△ECF，代入求出即可．

解答：解：如图3，

∵矩形纸片ABCD，AB=8，AD=6．将纸片折叠，使得AD边落在AB边上，
∴AD=6，CE=DB=8-6=2，BA=6-2=4，BC=6，
∵四边形ABCD是矩形，
∴AD∥CE，
∴△ABF∽△ECF，
∴

AB

EC

=

BF

CF

，
∴

4

2

=

6-CF

CF

，
∴CF=2，
故答案为：2．

点评：本题考查了折叠的性质，矩形的性质，相似三角形的性质和判定的应用，解此题的关键是求出各个边的长度和求出△ABF∽△ECF．