��Ŀ����
����ѧ��ѧϰ�����У����Ǿ��������µ�̽�����̽��������⣮
��ѧ���⣺��������3�����㣬����������ڲ��ٻ�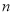 ���㣬������
���㣬������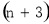 ����Ϊ���㻭�����Σ���ô���Լ��ö��ٸ������������Σ�
����Ϊ���㻭�����Σ���ô���Լ��ö��ٸ������������Σ�
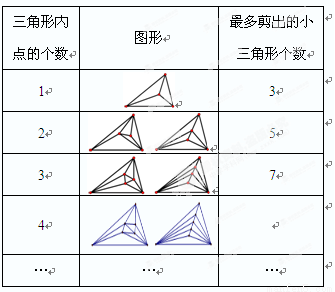
̽�����ɣ�Ϊ�˽��������⣬���ǿ��Դ� ��
��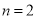 ��
�� �Ⱦ���ġ����������֣�̽�������Լ��õ������θ����ı仯���ɣ�
�Ⱦ���ġ����������֣�̽�������Լ��õ������θ����ı仯���ɣ�
��1�������������������4����ʱ���ѱ���������
��2���㷢�ֵı仯�����ǣ� ��
��3�����룺���������ڵ�ĸ���Ϊ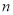 ʱ�������Լ��� �������Σ�
ʱ�������Լ��� �������Σ�
������ͨ���Լ����εĹ۲졢�����������һ���̽����������Ĺ��ɡ���������˼�뷽����Ϊ���ɣ�
�����������㳢���ù��ɵķ���̽����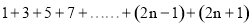 ���Ƕ��٣�
���Ƕ��٣�
��ϰ��ϵ�д�
�����Ŀ
�����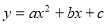 ��
��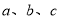 ������
Ϊ������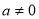 ���е�
���е� ��
��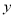 �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�����˽��ۣ�
��1�����κ��� ����Сֵ����СֵΪ
����Сֵ����СֵΪ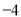 ��
��
��2����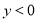 ����
����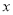 ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ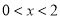 ��
��
��3�����κ��� ��ͼ����
��ͼ����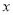 �����������㣬�����Ƿֱ���
�����������㣬�����Ƿֱ���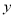 �����࣮
�����࣮
��������ȷ���۵ĸ����� �� ��
 B��
B�� C��
C�� D��
D��



 ��һԪ���η���
��һԪ���η��� ��ʵ��������
��ʵ�������� ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� �� 



















 ��b=��
��b=�� ����8�֣�
����8�֣�
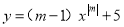 ��y����x��һ�κ�������m=______��
��y����x��һ�κ�������m=______��