题目内容
 如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为
如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为
- A.

- B.
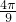
- C.

- D.

A
分析:连接OA,OB,则OA⊥AP,OB⊥PB.在四边形APBO中利用内角和定理即可求得∠AOB的度数,进而求得∠ACB的度数,从而求得∠ACB的弧度数.
解答: 解:连接OA,OB.则OA⊥AP,OB⊥PB,
解:连接OA,OB.则OA⊥AP,OB⊥PB,
∴在四边形APBO中,∠P+∠AOB=180°,
又∵∠AOB=2∠ACB,∠ABC=2∠P,
设∠ACB=180°-2∠ABC=180°-4∠P,
∴∠AOB=360°-8∠P,
∴∠P+∠AOB=∠P+(360°-8∠P)=180°,
∴∠P= ,
,
∴∠ACB=180-4× =
= ,
,
∴∠ACB的弧度数为 .
.
故选A.
点评:本题主要考查了切线的性质定理,以及等腰三角形的性质定理,根据性质定理正确求得∠AOB的度数是解决本题的关键.
分析:连接OA,OB,则OA⊥AP,OB⊥PB.在四边形APBO中利用内角和定理即可求得∠AOB的度数,进而求得∠ACB的度数,从而求得∠ACB的弧度数.
解答:
 解:连接OA,OB.则OA⊥AP,OB⊥PB,
解:连接OA,OB.则OA⊥AP,OB⊥PB,∴在四边形APBO中,∠P+∠AOB=180°,
又∵∠AOB=2∠ACB,∠ABC=2∠P,
设∠ACB=180°-2∠ABC=180°-4∠P,
∴∠AOB=360°-8∠P,
∴∠P+∠AOB=∠P+(360°-8∠P)=180°,
∴∠P=
 ,
,∴∠ACB=180-4×
 =
= ,
,∴∠ACB的弧度数为
 .
.故选A.
点评:本题主要考查了切线的性质定理,以及等腰三角形的性质定理,根据性质定理正确求得∠AOB的度数是解决本题的关键.

练习册系列答案
相关题目
 如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为( )
如图△ABC内接于⊙O,PA,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,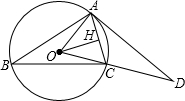 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
 如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.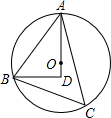 已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=
已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=