题目内容
 已知:如图中,AD是∠A的角平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
已知:如图中,AD是∠A的角平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.考点:菱形的判定
专题:证明题
分析:由已知易得四边形AEDF是平行四边形,由角平分线和平行线的定义可得∠FAD=∠FDA,根据AF=DF得到四边形AEDF是菱形.
解答:证明:∵AD是△ABC的角平分线,∴∠EAD=∠FAD,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∴∠FAD=∠FDA
∴AF=DF,
∴四边形AEDF是菱形.
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∴∠FAD=∠FDA
∴AF=DF,
∴四边形AEDF是菱形.
点评:此题主要考查菱形的判定,有一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
在算式am+n÷( )=am-2中,括号内的代数式应是( )
| A、am+n-2 |
| B、an-2 |
| C、am+n+3 |
| D、an+2 |
已知菱形的周长为40cm,一条对角线长为16cm,则这个菱形的面积为( )cm2.
| A、108 | B、114 |
| C、64 | D、96 |
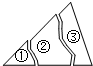 如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带第( )块到玻璃店去.
如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带第( )块到玻璃店去.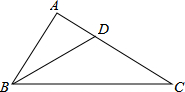 已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.
已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.