题目内容
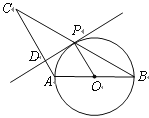
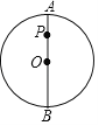
【题目】如图，AB是⊙O的直径，点P是AB上一点，且点P是弦CD的中点．
（1）依题意画出弦CD，并说明画图的依据；（不写画法，保留画图痕迹）
（2）若AP＝2，CD＝8，求⊙O的半径．
【答案】（1）画图见解析，依据：平分弦（非直径）的直径垂直于弦；（2）⊙O的半径为5．
【解析】
（1）过P点作AB的垂线即可，作图依据是垂径定理的推论．
（2）设⊙O的半径为r，在Rt△OPD中，利用勾股定理构建方程即可解决问题．
（1）过P点作AB的垂线交圆与C、D两点， CD就是所求的弦，如图．
依据：平分弦（非直径）的直径垂直于弦；
（2）如图，连接OD，
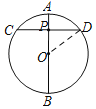
∵OA⊥CD于点P，AB是⊙O的直径，
∴∠OPD＝90°，PD＝
CD，
∵CD＝8，
∴PD＝4．
设⊙O的半径为r，则OD＝r，OP＝OA﹣AP＝r﹣2，
在Rt△ODP中，∠OPD＝90°，
∴OD2＝OP2+PD2，
即r2＝（r﹣2）2+42，
解得r＝5，
即⊙O的半径为5．
【题目】丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获得了两个班的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．
①A、B两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成5组：x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100）：
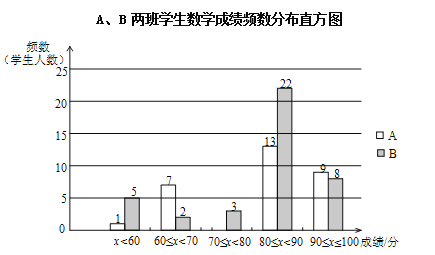
②A、B两班学生测试成绩在80≤x<90这一组的数据如下：
A班：80 80 82 83 85 85 86 87 87 87 88 89 89
B班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下：
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息，回答下列问题：
（1）补全数学成绩频数分布直方图；
（2）写出表中m、n的值；
（3）请你对比分析A、B两班学生的数学学习情况（至少从两个不同的角度分析）．
